ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

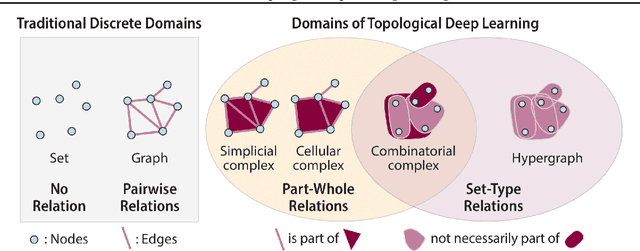
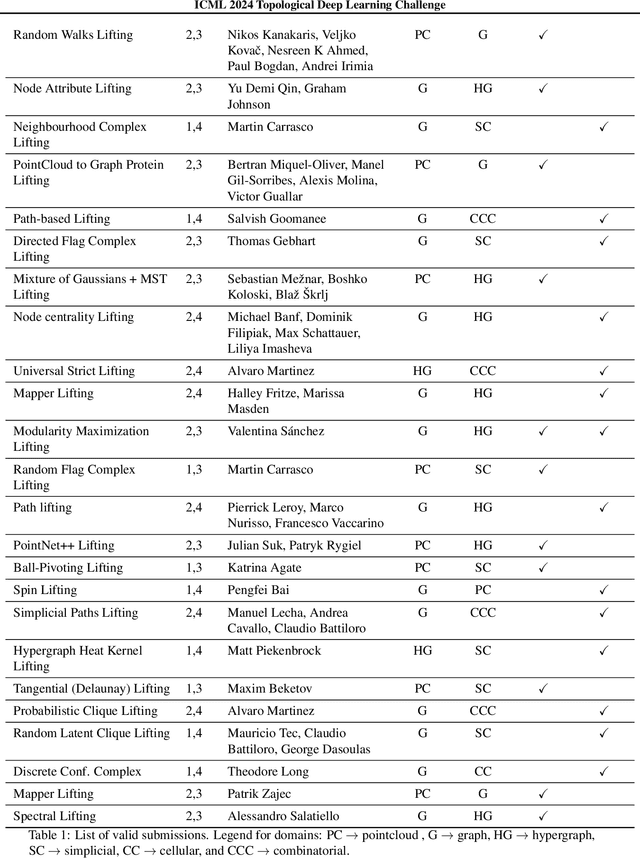
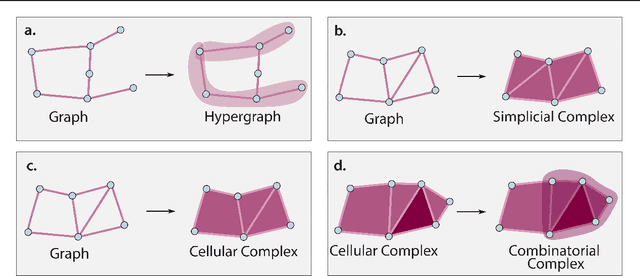
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

Topology-Informed Graph Transformer

Transformers have revolutionized performance in Natural Language Processing and Vision, paving the way for their integration with Graph Neural Networks (GNNs). One key challenge in enhancing graph transformers is strengthening the discriminative power of distinguishing isomorphisms of graphs, which plays a crucial role in boosting their predictive performances. To address this challenge, we introduce 'Topology-Informed Graph Transformer (TIGT)', a novel transformer enhancing both discriminative power in detecting graph isomorphisms and the overall performance of Graph Transformers. TIGT consists of four components: A topological positional embedding layer using non-isomorphic universal covers based on cyclic subgraphs of graphs to ensure unique graph representation: A dual-path message-passing layer to explicitly encode topological characteristics throughout the encoder layers: A global attention mechanism: And a graph information layer to recalibrate channel-wise graph features for better feature representation. TIGT outperforms previous Graph Transformers in classifying synthetic dataset aimed at distinguishing isomorphism classes of graphs. Additionally, mathematical analysis and empirical evaluations highlight our model's competitive edge over state-of-the-art Graph Transformers across various benchmark datasets.

A Gated MLP Architecture for Learning Topological Dependencies in Spatio-Temporal Graphs

Graph Neural Networks (GNNs) and Transformer have been increasingly adopted to learn the complex vector representations of spatio-temporal graphs, capturing intricate spatio-temporal dependencies crucial for applications such as traffic datasets. Although many existing methods utilize multi-head attention mechanisms and message-passing neural networks (MPNNs) to capture both spatial and temporal relations, these approaches encode temporal and spatial relations independently, and reflect the graph's topological characteristics in a limited manner. In this work, we introduce the Cycle to Mixer (Cy2Mixer), a novel spatio-temporal GNN based on topological non-trivial invariants of spatio-temporal graphs with gated multi-layer perceptrons (gMLP). The Cy2Mixer is composed of three blocks based on MLPs: A message-passing block for encapsulating spatial information, a cycle message-passing block for enriching topological information through cyclic subgraphs, and a temporal block for capturing temporal properties. We bolster the effectiveness of Cy2Mixer with mathematical evidence emphasizing that our cycle message-passing block is capable of offering differentiated information to the deep learning model compared to the message-passing block. Furthermore, empirical evaluations substantiate the efficacy of the Cy2Mixer, demonstrating state-of-the-art performances across various traffic benchmark datasets.

Model-Free Reconstruction of Capacity Degradation Trajectory of Lithium-Ion Batteries Using Early Cycle Data

Early degradation prediction of lithium-ion batteries is crucial for ensuring safety and preventing unexpected failure in manufacturing and diagnostic processes. Long-term capacity trajectory predictions can fail due to cumulative errors and noise. To address this issue, this study proposes a data-centric method that uses early single-cycle data to predict the capacity degradation trajectory of lithium-ion cells. The method involves predicting a few knots at specific retention levels using a deep learning-based model and interpolating them to reconstruct the trajectory. Two approaches are used to identify the retention levels of two to four knots: uniformly dividing the retention up to the end of life and finding optimal locations using Bayesian optimization. The proposed model is validated with experimental data from 169 cells using five-fold cross-validation. The results show that mean absolute percentage errors in trajectory prediction are less than 1.60% for all cases of knots. By predicting only the cycle numbers of at least two knots based on early single-cycle charge and discharge data, the model can directly estimate the overall capacity degradation trajectory. Further experiments suggest using three-cycle input data to achieve robust and efficient predictions, even in the presence of noise. The method is then applied to predict various shapes of capacity degradation patterns using additional experimental data from 82 cells. The study demonstrates that collecting only the cycle information of a few knots during model training and a few early cycle data points for predictions is sufficient for predicting capacity degradation. This can help establish appropriate warranties or replacement cycles in battery manufacturing and diagnosis processes.

The PWLR Graph Representation: A Persistent Weisfeiler-Lehman scheme with Random Walks for Graph Classification

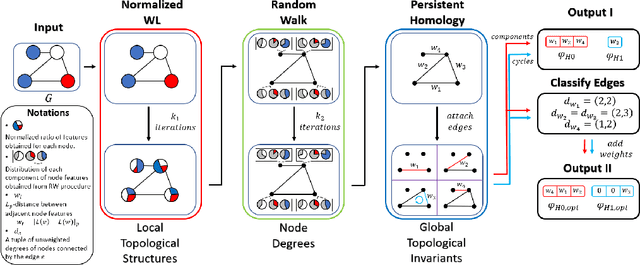
This paper presents the Persistent Weisfeiler-Lehman Random walk scheme (abbreviated as PWLR) for graph representations, a novel mathematical framework which produces a collection of explainable low-dimensional representations of graphs with discrete and continuous node features. The proposed scheme effectively incorporates normalized Weisfeiler-Lehman procedure, random walks on graphs, and persistent homology. We thereby integrate three distinct properties of graphs, which are local topological features, node degrees, and global topological invariants, while preserving stability from graph perturbations. This generalizes many variants of Weisfeiler-Lehman procedures, which are primarily used to embed graphs with discrete node labels. Empirical results suggest that these representations can be efficiently utilized to produce comparable results to state-of-the-art techniques in classifying graphs with discrete node labels, and enhanced performances in classifying those with continuous node features.

Impedance-based Capacity Estimation for Lithium-Ion Batteries Using Generative Adversarial Network

This paper proposes a fully unsupervised methodology for the reliable extraction of latent variables representing the characteristics of lithium-ion batteries (LIBs) from electrochemical impedance spectroscopy (EIS) data using information maximizing generative adversarial networks. Meaningful representations can be obtained from EIS data even when measured with direct current and without relaxation, which are difficult to express when using circuit models. The extracted latent variables were investigated as capacity degradation progressed and were used to estimate the discharge capacity of the batteries by employing Gaussian process regression. The proposed method was validated under various conditions of EIS data during charging and discharging. The results indicate that the proposed model provides more robust capacity estimations than the direct capacity estimations obtained from EIS. We demonstrate that the latent variables extracted from the EIS data measured with direct current and without relaxation reliably represent the degradation characteristics of LIBs.