Woo Chang Kim
Prediction Loss Guided Decision-Focused Learning
Sep 10, 2025Abstract:Decision-making under uncertainty is often considered in two stages: predicting the unknown parameters, and then optimizing decisions based on predictions. While traditional prediction-focused learning (PFL) treats these two stages separately, decision-focused learning (DFL) trains the predictive model by directly optimizing the decision quality in an end-to-end manner. However, despite using exact or well-approximated gradients, vanilla DFL often suffers from unstable convergence due to its flat-and-sharp loss landscapes. In contrast, PFL yields more stable optimization, but overlooks the downstream decision quality. To address this, we propose a simple yet effective approach: perturbing the decision loss gradient using the prediction loss gradient to construct an update direction. Our method requires no additional training and can be integrated with any DFL solvers. Using the sigmoid-like decaying parameter, we let the prediction loss gradient guide the decision loss gradient to train a predictive model that optimizes decision quality. Also, we provide a theoretical convergence guarantee to Pareto stationary point under mild assumptions. Empirically, we demonstrate our method across three stochastic optimization problems, showing promising results compared to other baselines. We validate that our approach achieves lower regret with more stable training, even in situations where either PFL or DFL struggles.
Contextual Scenario Generation for Two-Stage Stochastic Programming
Feb 07, 2025


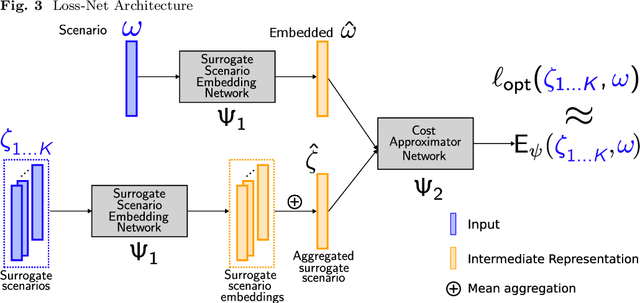
Abstract:Two-stage stochastic programs (2SPs) are important tools for making decisions under uncertainty. Decision-makers use contextual information to generate a set of scenarios to represent the true conditional distribution. However, the number of scenarios required is a barrier to implementing 2SPs, motivating the problem of generating a small set of surrogate scenarios that yield high-quality decisions when they represent uncertainty. Current scenario generation approaches do not leverage contextual information or do not address computational concerns. In response, we propose contextual scenario generation (CSG) to learn a mapping between the context and a set of surrogate scenarios of user-specified size. First, we propose a distributional approach that learns the mapping by minimizing a distributional distance between the predicted surrogate scenarios and the true contextual distribution. Second, we propose a task-based approach that aims to produce surrogate scenarios that yield high-quality decisions. The task-based approach uses neural architectures to approximate the downstream objective and leverages the approximation to search for the mapping. The proposed approaches apply to various problem structures and loosely only require efficient solving of the associated subproblems and 2SPs defined on the reduced scenario sets. Numerical experiments demonstrating the effectiveness of the proposed methods are presented.
Transformer-based Stagewise Decomposition for Large-Scale Multistage Stochastic Optimization
Apr 03, 2024Abstract:Solving large-scale multistage stochastic programming (MSP) problems poses a significant challenge as commonly used stagewise decomposition algorithms, including stochastic dual dynamic programming (SDDP), face growing time complexity as the subproblem size and problem count increase. Traditional approaches approximate the value functions as piecewise linear convex functions by incrementally accumulating subgradient cutting planes from the primal and dual solutions of stagewise subproblems. Recognizing these limitations, we introduce TranSDDP, a novel Transformer-based stagewise decomposition algorithm. This innovative approach leverages the structural advantages of the Transformer model, implementing a sequential method for integrating subgradient cutting planes to approximate the value function. Through our numerical experiments, we affirm TranSDDP's effectiveness in addressing MSP problems. It efficiently generates a piecewise linear approximation for the value function, significantly reducing computation time while preserving solution quality, thus marking a promising progression in the treatment of large-scale multistage stochastic programming problems.
ICLN: Input Convex Loss Network for Decision Focused Learning
Mar 04, 2024


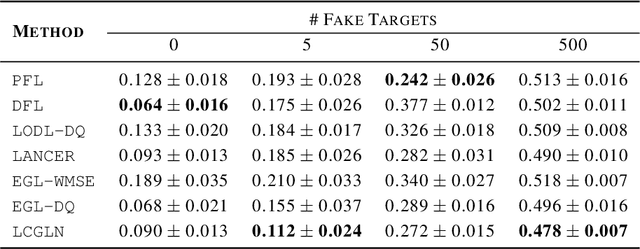
Abstract:In decision-making problem under uncertainty, predicting unknown parameters is often considered independent of the optimization part. Decision-focused Learning (DFL) is a task-oriented framework to integrate prediction and optimization by adapting predictive model to give better decision for the corresponding task. Here, an inevitable challenge arises when computing gradients of the optimal decision with respect to the parameters. Existing researches cope this issue by smoothly reforming surrogate optimization or construct surrogate loss function that mimic task loss. However, they are applied to restricted optimization domain or build functions in a local manner leading a large computational time. In this paper, we propose Input Convex Loss Network (ICLN), a novel global surrogate loss which can be implemented in a general DFL paradigm. ICLN learns task loss via Input Convex Neural Networks which is guaranteed to be convex for some inputs, while keeping the global structure for the other inputs. This enables ICLN to admit general DFL through only a single surrogate loss without any sense for choosing appropriate parametric forms. We confirm effectiveness and flexibility of ICLN by evaluating our proposed model with three stochastic decision-making problems.
Encoding Temporal Statistical-space Priors via Augmented Representation
Feb 03, 2024

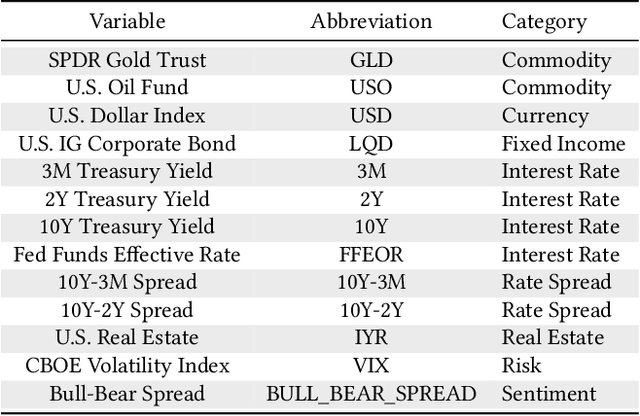

Abstract:Modeling time series data remains a pervasive issue as the temporal dimension is inherent to numerous domains. Despite significant strides in time series forecasting, high noise-to-signal ratio, non-normality, non-stationarity, and lack of data continue challenging practitioners. In response, we leverage a simple representation augmentation technique to overcome these challenges. Our augmented representation acts as a statistical-space prior encoded at each time step. In response, we name our method Statistical-space Augmented Representation (SSAR). The underlying high-dimensional data-generating process inspires our representation augmentation. We rigorously examine the empirical generalization performance on two data sets with two downstream temporal learning algorithms. Our approach significantly beats all five up-to-date baselines. Moreover, the highly modular nature of our approach can easily be applied to various settings. Lastly, fully-fledged theoretical perspectives are available throughout the writing for a clear and rigorous understanding.
Provably Scalable Black-Box Variational Inference with Structured Variational Families
Jan 19, 2024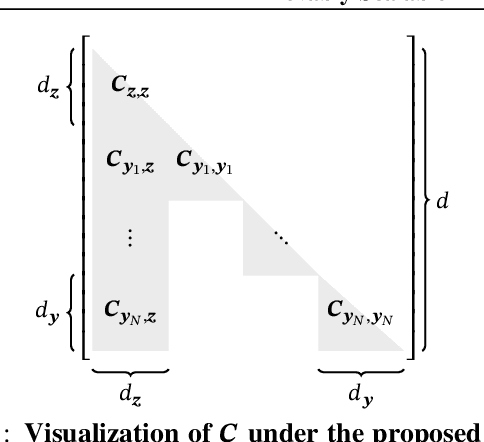



Abstract:Variational families with full-rank covariance approximations are known not to work well in black-box variational inference (BBVI), both empirically and theoretically. In fact, recent computational complexity results for BBVI have established that full-rank variational families scale poorly with the dimensionality of the problem compared to e.g. mean field families. This is particularly critical to hierarchical Bayesian models with local variables; their dimensionality increases with the size of the datasets. Consequently, one gets an iteration complexity with an explicit $\mathcal{O}(N^2)$ dependence on the dataset size $N$. In this paper, we explore a theoretical middle ground between mean-field variational families and full-rank families: structured variational families. We rigorously prove that certain scale matrix structures can achieve a better iteration complexity of $\mathcal{O}(N)$, implying better scaling with respect to $N$. We empirically verify our theoretical results on large-scale hierarchical models.
Curriculum Learning and Imitation Learning for Model-free Control on Financial Time-series
Nov 22, 2023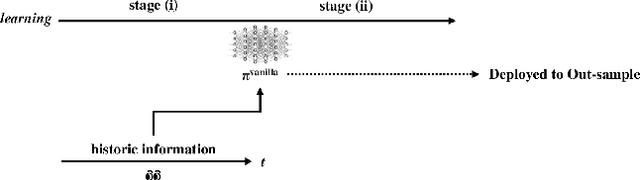

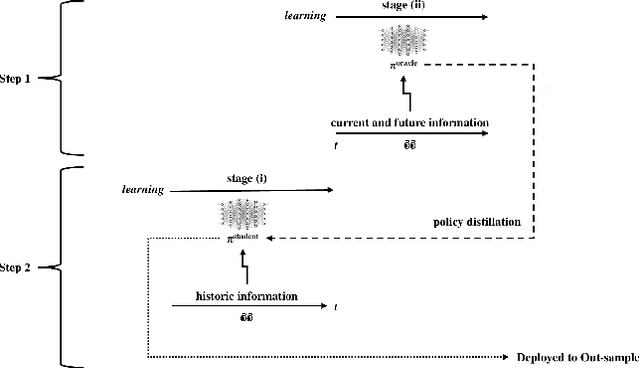
Abstract:Curriculum learning and imitation learning have been leveraged extensively in the robotics domain. However, minimal research has been done on leveraging these ideas on control tasks over highly stochastic time-series data. Here, we theoretically and empirically explore these approaches in a representative control task over complex time-series data. We implement the fundamental ideas of curriculum learning via data augmentation, while imitation learning is implemented via policy distillation from an oracle. Our findings reveal that curriculum learning should be considered a novel direction in improving control-task performance over complex time-series. Our ample random-seed out-sample empirics and ablation studies are highly encouraging for curriculum learning for time-series control. These findings are especially encouraging as we tune all overlapping hyperparameters on the baseline -- giving an advantage to the baseline. On the other hand, we find that imitation learning should be used with caution.
Mean-Variance Efficient Collaborative Filtering for Stock Recommendation
Jun 11, 2023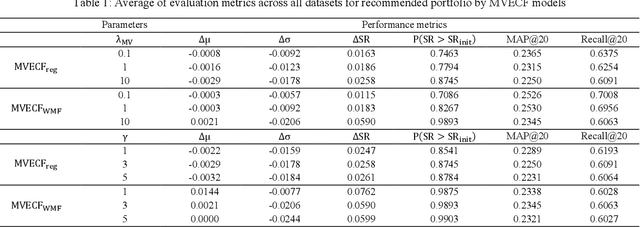
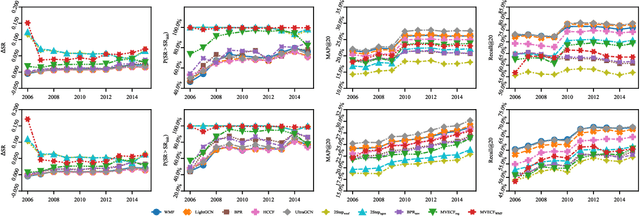


Abstract:The rise of FinTech has transformed financial services onto online platforms, yet stock investment recommender systems have received limited attention compared to other industries. Personalized stock recommendations can significantly impact customer engagement and satisfaction within the industry. However, traditional investment recommendations focus on high-return stocks or highly diversified portfolios based on the modern portfolio theory, often neglecting user preferences. On the other hand, collaborative filtering (CF) methods also may not be directly applicable to stock recommendations, because it is inappropriate to just recommend stocks that users like. The key is to optimally blend users preference with the portfolio theory. However, research on stock recommendations within the recommender system domain remains comparatively limited, and no existing model considers both the preference of users and the risk-return characteristics of stocks. In this regard, we propose a mean-variance efficient collaborative filtering (MVECF) model for stock recommendations that consider both aspects. Our model is specifically designed to improve the pareto optimality (mean-variance efficiency) in a trade-off between the risk (variance of return) and return (mean return) by systemically handling uncertainties in stock prices. Such improvements are incorporated into the MVECF model using regularization, and the model is restructured to fit into the ordinary matrix factorization scheme to boost computational efficiency. Experiments on real-world fund holdings data show that our model can increase the mean-variance efficiency of suggested portfolios while sacrificing just a small amount of mean average precision and recall. Finally, we further show MVECF is easily applicable to the state-of-the-art graph-based ranking models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge