New bounds on the cohesion of complete-link and other linkage methods for agglomeration clustering

Linkage methods are among the most popular algorithms for hierarchical clustering. Despite their relevance the current knowledge regarding the quality of the clustering produced by these methods is limited. Here, we improve the currently available bounds on the maximum diameter of the clustering obtained by complete-link for metric spaces. One of our new bounds, in contrast to the existing ones, allows us to separate complete-link from single-link in terms of approximation for the diameter, which corroborates the common perception that the former is more suitable than the latter when the goal is producing compact clusters. We also show that our techniques can be employed to derive upper bounds on the cohesion of a class of linkage methods that includes the quite popular average-link.

Time-Constrained Learning

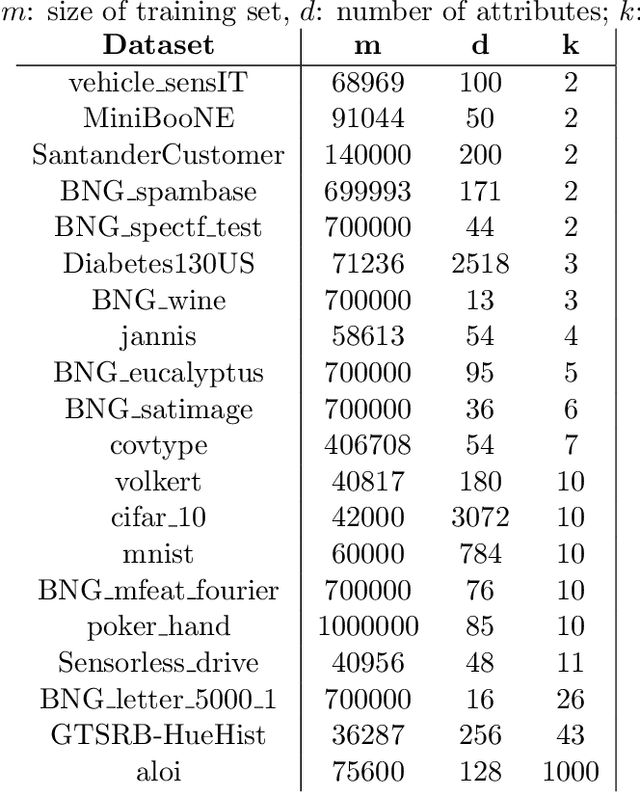
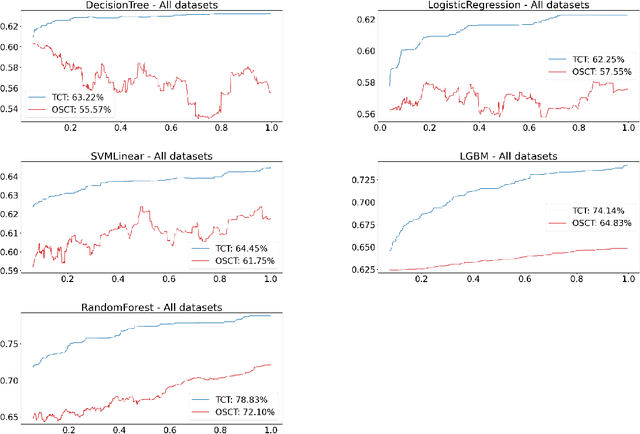
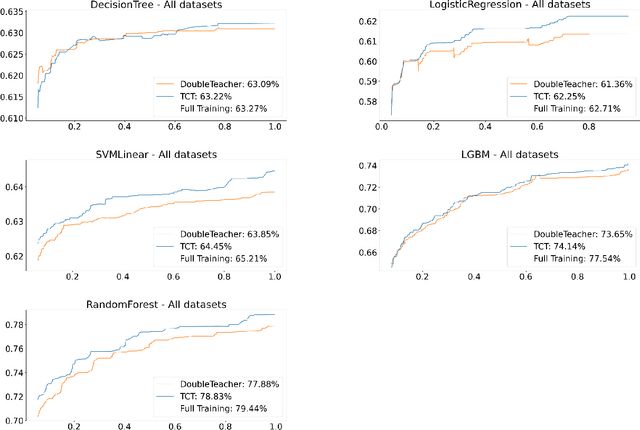
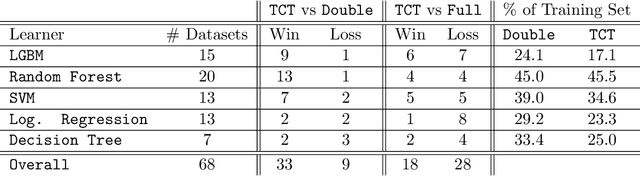
Consider a scenario in which we have a huge labeled dataset ${\cal D}$ and a limited time to train some given learner using ${\cal D}$. Since we may not be able to use the whole dataset, how should we proceed? Questions of this nature motivate the definition of the Time-Constrained Learning Task (TCL): Given a dataset ${\cal D}$ sampled from an unknown distribution $\mu$, a learner ${\cal L}$ and a time limit $T$, the goal is to obtain in at most $T$ units of time the classification model with highest possible accuracy w.r.t. to $\mu$, among those that can be built by ${\cal L}$ using the dataset ${\cal D}$. We propose TCT, an algorithm for the TCL task designed based that on principles from Machine Teaching. We present an experimental study involving 5 different Learners and 20 datasets where we show that TCT consistently outperforms two other algorithms: the first is a Teacher for black-box learners proposed in [Dasgupta et al., ICML 19] and the second is a natural adaptation of random sampling for the TCL setting. We also compare TCT with Stochastic Gradient Descent training -- our method is again consistently better. While our work is primarily practical, we also show that a stripped-down version of TCT has provable guarantees. Under reasonable assumptions, the time our algorithm takes to achieve a certain accuracy is never much bigger than the time it takes the batch teacher (which sends a single batch of examples) to achieve similar accuracy, and in some case it is almost exponentially better.

Shallow decision trees for explainable $k$-means clustering

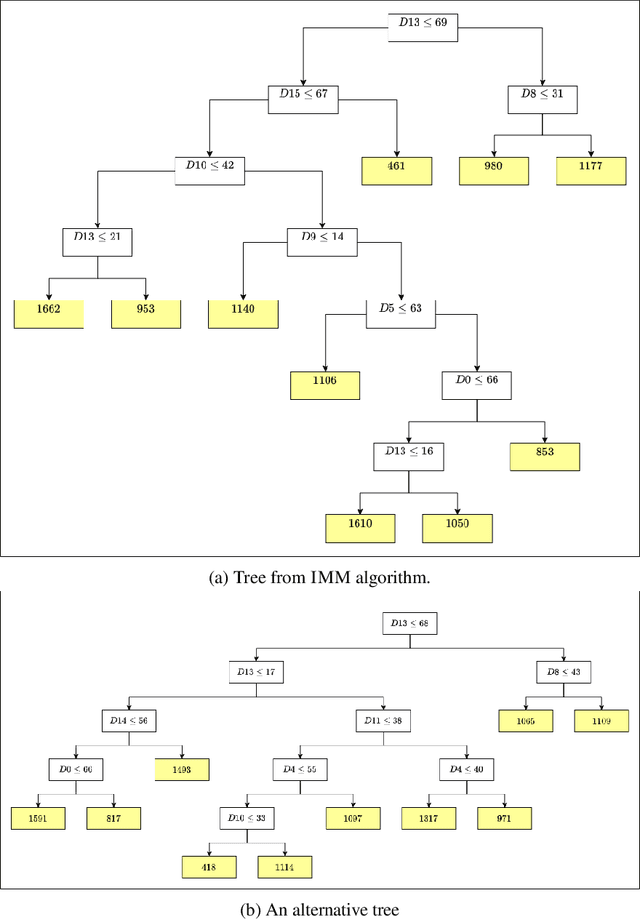
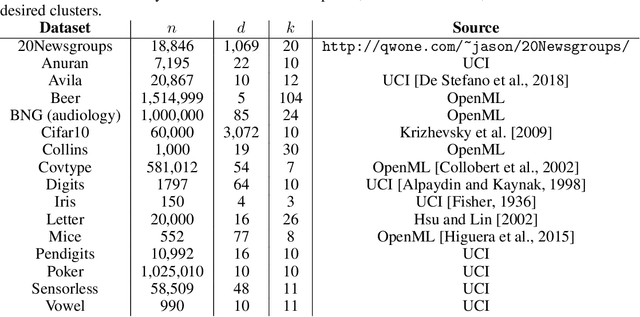
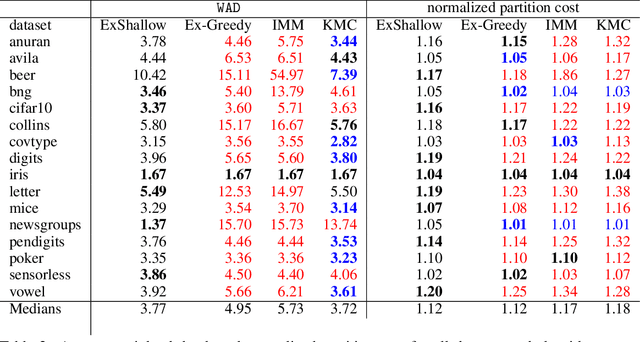
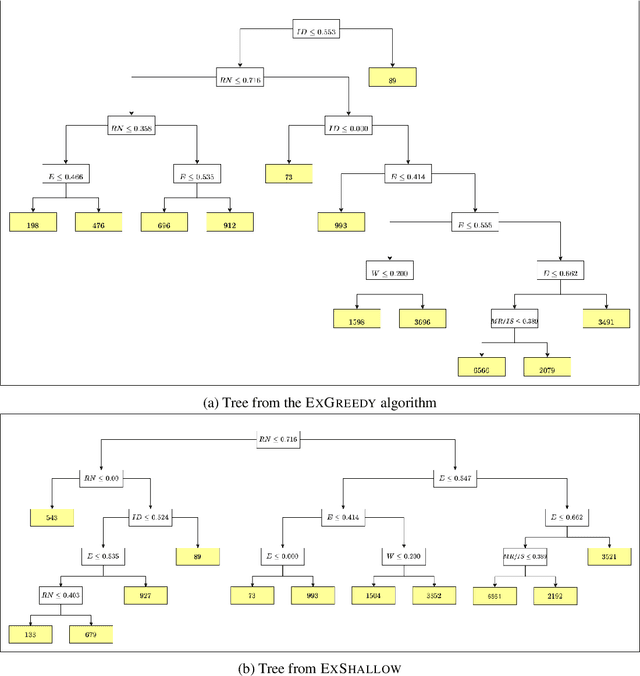
A number of recent works have employed decision trees for the construction of explainable partitions that aim to minimize the $k$-means cost function. These works, however, largely ignore metrics related to the depths of the leaves in the resulting tree, which is perhaps surprising considering how the explainability of a decision tree depends on these depths. To fill this gap in the literature, we propose an efficient algorithm that takes into account these metrics. In experiments on 16 datasets, our algorithm yields better results than decision-tree clustering algorithms such as the ones presented in \cite{dasgupta2020explainable}, \cite{frost2020exkmc}, \cite{laber2021price} and \cite{DBLP:conf/icml/MakarychevS21}, typically achieving lower or equivalent costs with considerably shallower trees. We also show, through a simple adaptation of existing techniques, that the problem of building explainable partitions induced by binary trees for the $k$-means cost function does not admit an $(1+\epsilon)$-approximation in polynomial time unless $P=NP$, which justifies the quest for approximation algorithms and/or heuristics.

On the price of explainability for some clustering problems

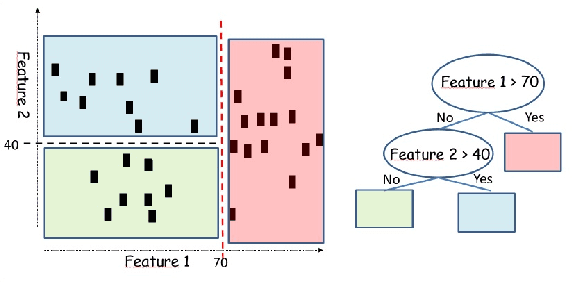
Machine learning models and algorithms are used in a number of systems that affect our daily life. Thus, in some settings, methods that are easy to explain or interpret may be highly desirable. The price of explainability can be thought of as the loss in terms of quality that is unavoidable if we restrict these systems to use explainable methods. We study the price of explainability, under a theoretical perspective, for clustering tasks. We provide upper and lower bounds on this price as well as efficient algorithms to build explainable clustering for the $k$-means, $k$-medians, $k$-center and the maximum-spacing problems in a natural model in which explainability is achieved via decision trees.

Speeding up Word Mover's Distance and its variants via properties of distances between embeddings

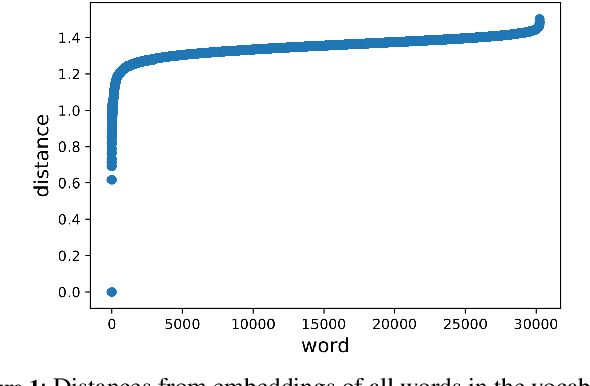
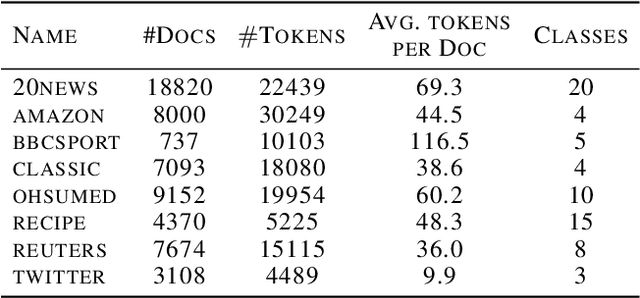
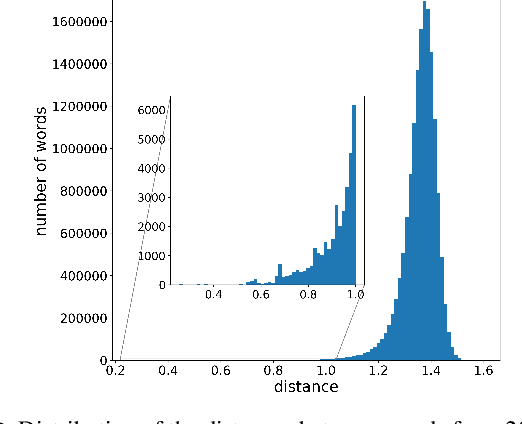
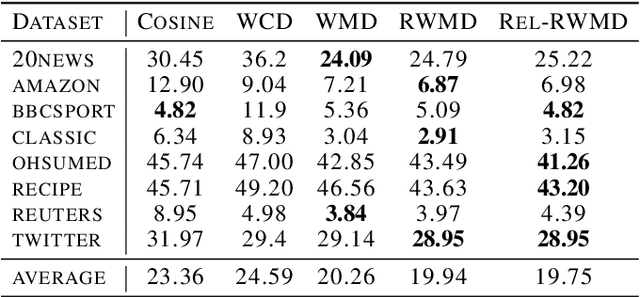
The Word Mover's Distance (WMD) proposed in Kusner et al. [ICML,2015] is a distance between documents that takes advantage of semantic relations among words that are captured by their embeddings. This distance proved to be quite effective, obtaining state-of-art error rates for classification tasks, but also impracticable for large collections/documents due to its computational complexity. For circumventing this problem, variants of WMD have been proposed. Among them, Relaxed Word Mover's Distance (RWMD) is one of the most successful due to its simplicity, effectiveness, and also because of its fast implementations. Relying on assumptions that are supported by empirical properties of the distances between embeddings, we propose an approach to speed up both WMD and RWMD. Experiments over 10 datasets suggest that our approach leads to a significant speed-up in document classification tasks while maintaining the same error rates.

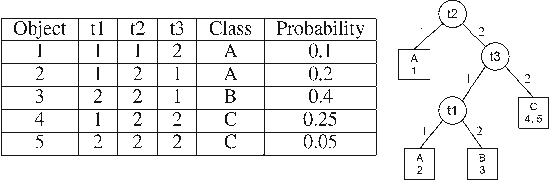
Decision Trees for Function Evaluation - Simultaneous Optimization of Worst and Expected Cost

In several applications of automatic diagnosis and active learning a central problem is the evaluation of a discrete function by adaptively querying the values of its variables until the values read uniquely determine the value of the function. In general, the process of reading the value of a variable might involve some cost, computational or even a fee to be paid for the experiment required for obtaining the value. This cost should be taken into account when deciding the next variable to read. The goal is to design a strategy for evaluating the function incurring little cost (in the worst case or in expectation according to a prior distribution on the possible variables' assignments). Our algorithm builds a strategy (decision tree) which attains a logarithmic approxima- tion simultaneously for the expected and worst cost spent. This is best possible under the assumption that $P \neq NP.$