Lucas Murtinho
Optimization of Inter-group Criteria for Clustering with Minimum Size Constraints
Jan 13, 2024Abstract:Internal measures that are used to assess the quality of a clustering usually take into account intra-group and/or inter-group criteria. There are many papers in the literature that propose algorithms with provable approximation guarantees for optimizing the former. However, the optimization of inter-group criteria is much less understood. Here, we contribute to the state-of-the-art of this literature by devising algorithms with provable guarantees for the maximization of two natural inter-group criteria, namely the minimum spacing and the minimum spanning tree spacing. The former is the minimum distance between points in different groups while the latter captures separability through the cost of the minimum spanning tree that connects all groups. We obtain results for both the unrestricted case, in which no constraint on the clusters is imposed, and for the constrained case where each group is required to have a minimum number of points. Our constraint is motivated by the fact that the popular Single Linkage, which optimizes both criteria in the unrestricted case, produces clusterings with many tiny groups. To complement our work, we present an empirical study with 10 real datasets, providing evidence that our methods work very well in practical settings.
Shallow decision trees for explainable $k$-means clustering
Dec 29, 2021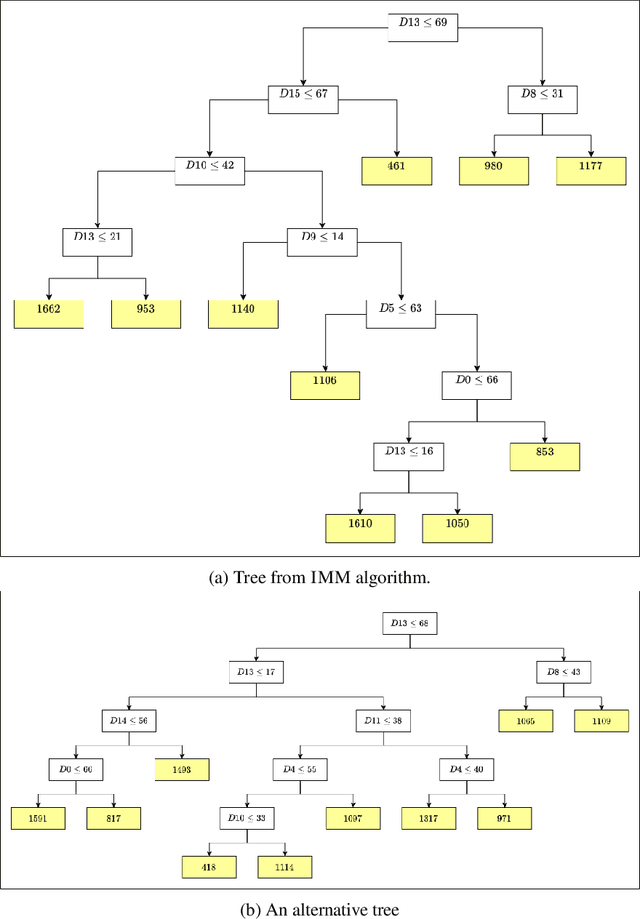
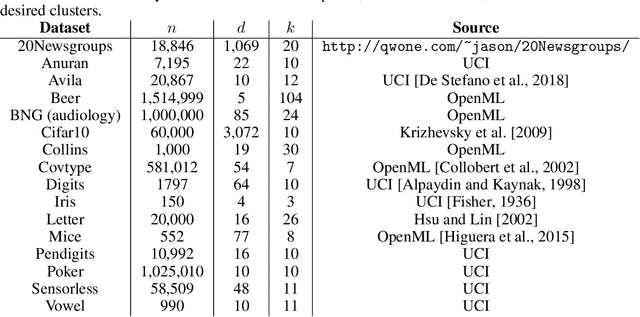
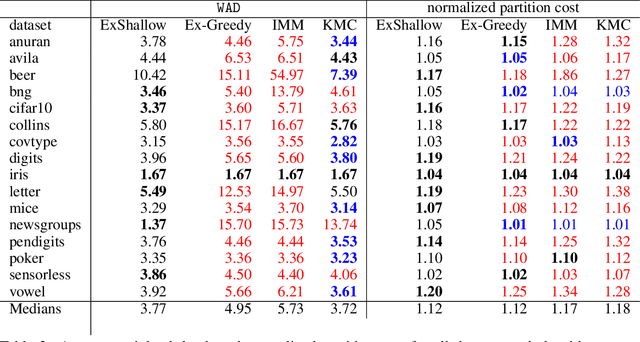
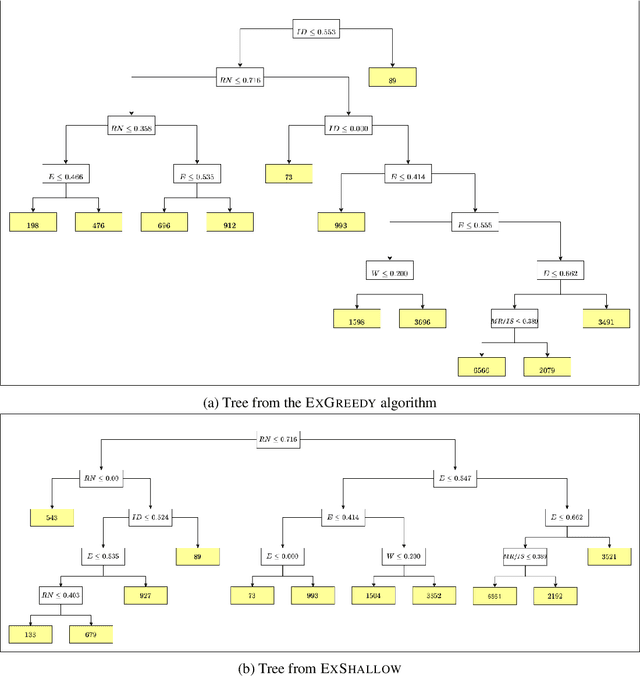
Abstract:A number of recent works have employed decision trees for the construction of explainable partitions that aim to minimize the $k$-means cost function. These works, however, largely ignore metrics related to the depths of the leaves in the resulting tree, which is perhaps surprising considering how the explainability of a decision tree depends on these depths. To fill this gap in the literature, we propose an efficient algorithm that takes into account these metrics. In experiments on 16 datasets, our algorithm yields better results than decision-tree clustering algorithms such as the ones presented in \cite{dasgupta2020explainable}, \cite{frost2020exkmc}, \cite{laber2021price} and \cite{DBLP:conf/icml/MakarychevS21}, typically achieving lower or equivalent costs with considerably shallower trees. We also show, through a simple adaptation of existing techniques, that the problem of building explainable partitions induced by binary trees for the $k$-means cost function does not admit an $(1+\epsilon)$-approximation in polynomial time unless $P=NP$, which justifies the quest for approximation algorithms and/or heuristics.
On the price of explainability for some clustering problems
Jan 05, 2021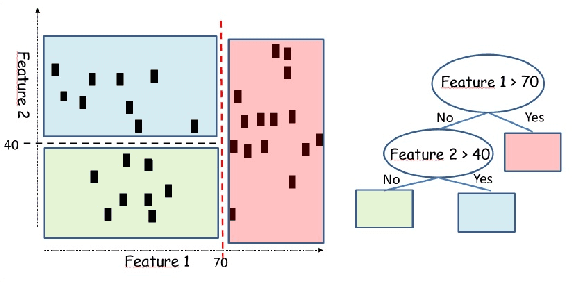
Abstract:Machine learning models and algorithms are used in a number of systems that affect our daily life. Thus, in some settings, methods that are easy to explain or interpret may be highly desirable. The price of explainability can be thought of as the loss in terms of quality that is unavoidable if we restrict these systems to use explainable methods. We study the price of explainability, under a theoretical perspective, for clustering tasks. We provide upper and lower bounds on this price as well as efficient algorithms to build explainable clustering for the $k$-means, $k$-medians, $k$-center and the maximum-spacing problems in a natural model in which explainability is achieved via decision trees.
Minimization of Gini impurity via connections with the k-means problem
Sep 28, 2018Abstract:The Gini impurity is one of the measures used to select attribute in Decision Trees/Random Forest construction. In this note we discuss connections between the problem of computing the partition with minimum Weighted Gini impurity and the $k$-means clustering problem. Based on these connections we show that the computation of the partition with minimum Weighted Gini is a NP-Complete problem and we also discuss how to obtain new algorithms with provable approximation for the Gini Minimization problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge