Shallow decision trees for explainable $k$-means clustering
Paper and Code
Dec 29, 2021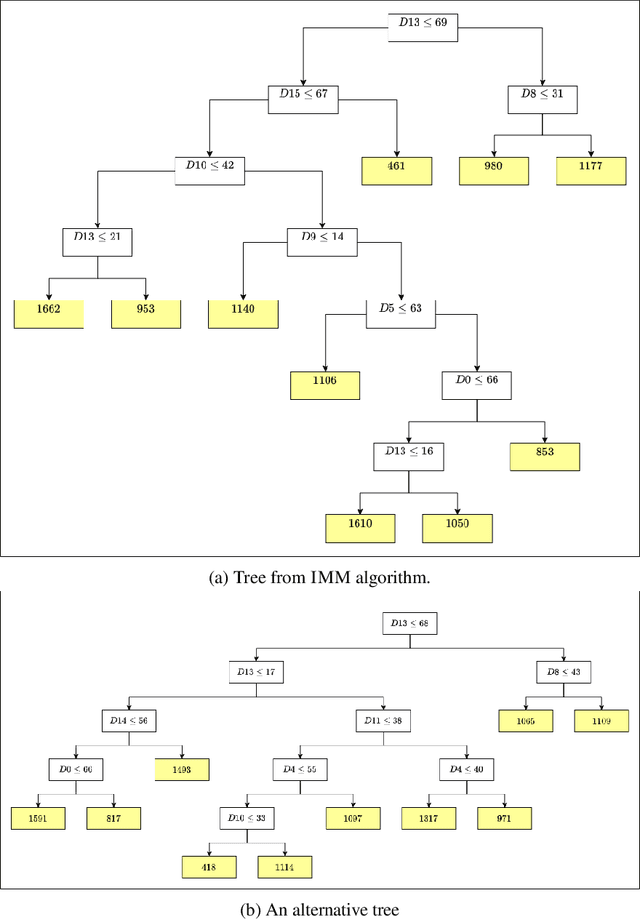
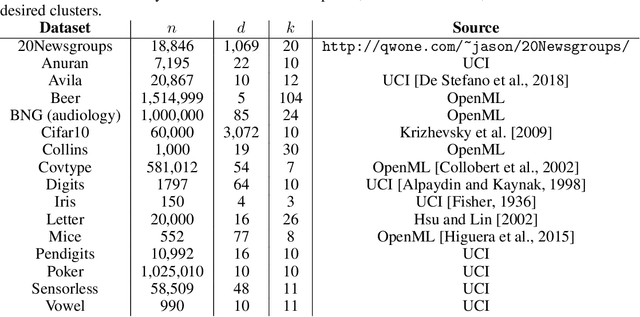
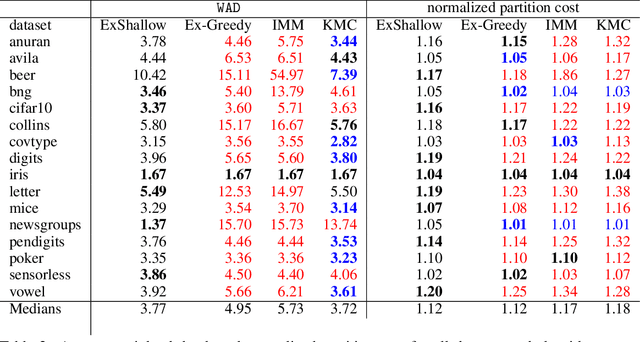
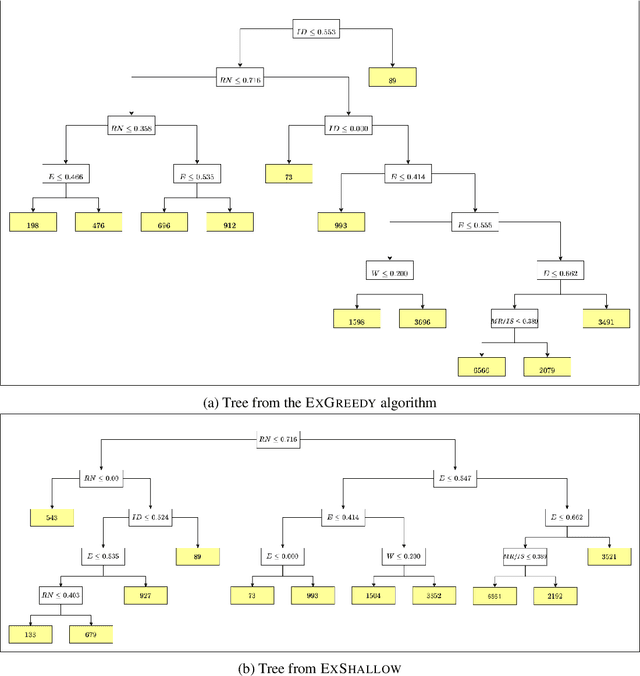
A number of recent works have employed decision trees for the construction of explainable partitions that aim to minimize the $k$-means cost function. These works, however, largely ignore metrics related to the depths of the leaves in the resulting tree, which is perhaps surprising considering how the explainability of a decision tree depends on these depths. To fill this gap in the literature, we propose an efficient algorithm that takes into account these metrics. In experiments on 16 datasets, our algorithm yields better results than decision-tree clustering algorithms such as the ones presented in \cite{dasgupta2020explainable}, \cite{frost2020exkmc}, \cite{laber2021price} and \cite{DBLP:conf/icml/MakarychevS21}, typically achieving lower or equivalent costs with considerably shallower trees. We also show, through a simple adaptation of existing techniques, that the problem of building explainable partitions induced by binary trees for the $k$-means cost function does not admit an $(1+\epsilon)$-approximation in polynomial time unless $P=NP$, which justifies the quest for approximation algorithms and/or heuristics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge