On the Probabilistic Learnability of Compact Neural Network Preimage Bounds

Although recent provable methods have been developed to compute preimage bounds for neural networks, their scalability is fundamentally limited by the #P-hardness of the problem. In this work, we adopt a novel probabilistic perspective, aiming to deliver solutions with high-confidence guarantees and bounded error. To this end, we investigate the potential of bootstrap-based and randomized approaches that are capable of capturing complex patterns in high-dimensional spaces, including input regions where a given output property holds. In detail, we introduce $\textbf{R}$andom $\textbf{F}$orest $\textbf{Pro}$perty $\textbf{Ve}$rifier ($\texttt{RF-ProVe}$), a method that exploits an ensemble of randomized decision trees to generate candidate input regions satisfying a desired output property and refines them through active resampling. Our theoretical derivations offer formal statistical guarantees on region purity and global coverage, providing a practical, scalable solution for computing compact preimage approximations in cases where exact solvers fail to scale.

Rigorous Probabilistic Guarantees for Robust Counterfactual Explanations

We study the problem of assessing the robustness of counterfactual explanations for deep learning models. We focus on $\textit{plausible model shifts}$ altering model parameters and propose a novel framework to reason about the robustness property in this setting. To motivate our solution, we begin by showing for the first time that computing the robustness of counterfactuals with respect to plausible model shifts is NP-complete. As this (practically) rules out the existence of scalable algorithms for exactly computing robustness, we propose a novel probabilistic approach which is able to provide tight estimates of robustness with strong guarantees while preserving scalability. Remarkably, and differently from existing solutions targeting plausible model shifts, our approach does not impose requirements on the network to be analyzed, thus enabling robustness analysis on a wider range of architectures. Experiments on four binary classification datasets indicate that our method improves the state of the art in generating robust explanations, outperforming existing methods on a range of metrics.

Enumerating Safe Regions in Deep Neural Networks with Provable Probabilistic Guarantees

Identifying safe areas is a key point to guarantee trust for systems that are based on Deep Neural Networks (DNNs). To this end, we introduce the AllDNN-Verification problem: given a safety property and a DNN, enumerate the set of all the regions of the property input domain which are safe, i.e., where the property does hold. Due to the #P-hardness of the problem, we propose an efficient approximation method called epsilon-ProVe. Our approach exploits a controllable underestimation of the output reachable sets obtained via statistical prediction of tolerance limits, and can provide a tight (with provable probabilistic guarantees) lower estimate of the safe areas. Our empirical evaluation on different standard benchmarks shows the scalability and effectiveness of our method, offering valuable insights for this new type of verification of DNNs.

The #DNN-Verification problem: Counting Unsafe Inputs for Deep Neural Networks

Deep Neural Networks are increasingly adopted in critical tasks that require a high level of safety, e.g., autonomous driving. While state-of-the-art verifiers can be employed to check whether a DNN is unsafe w.r.t. some given property (i.e., whether there is at least one unsafe input configuration), their yes/no output is not informative enough for other purposes, such as shielding, model selection, or training improvements. In this paper, we introduce the #DNN-Verification problem, which involves counting the number of input configurations of a DNN that result in a violation of a particular safety property. We analyze the complexity of this problem and propose a novel approach that returns the exact count of violations. Due to the #P-completeness of the problem, we also propose a randomized, approximate method that provides a provable probabilistic bound of the correct count while significantly reducing computational requirements. We present experimental results on a set of safety-critical benchmarks that demonstrate the effectiveness of our approximate method and evaluate the tightness of the bound.

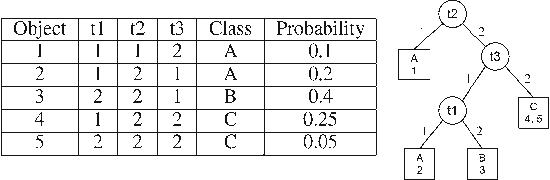
Decision Trees for Function Evaluation - Simultaneous Optimization of Worst and Expected Cost

In several applications of automatic diagnosis and active learning a central problem is the evaluation of a discrete function by adaptively querying the values of its variables until the values read uniquely determine the value of the function. In general, the process of reading the value of a variable might involve some cost, computational or even a fee to be paid for the experiment required for obtaining the value. This cost should be taken into account when deciding the next variable to read. The goal is to design a strategy for evaluating the function incurring little cost (in the worst case or in expectation according to a prior distribution on the possible variables' assignments). Our algorithm builds a strategy (decision tree) which attains a logarithmic approxima- tion simultaneously for the expected and worst cost spent. This is best possible under the assumption that $P \neq NP.$