Subsampling, aligning, and averaging to find circular coordinates in recurrent time series

We introduce a new algorithm for finding robust circular coordinates on data that is expected to exhibit recurrence, such as that which appears in neuronal recordings of C. elegans. Techniques exist to create circular coordinates on a simplicial complex from a dimension 1 cohomology class, and these can be applied to the Rips complex of a dataset when it has a prominent class in its dimension 1 cohomology. However, it is known this approach is extremely sensitive to uneven sampling density. Our algorithm comes with a new method to correct for uneven sampling density, adapting our prior work on averaging coordinates in manifold learning. We use rejection sampling to correct for inhomogeneous sampling and then apply Procrustes matching to align and average the subsamples. In addition to providing a more robust coordinate than other approaches, this subsampling and averaging approach has better efficiency. We validate our technique on both synthetic data sets and neuronal activity recordings. Our results reveal a topological model of neuronal trajectories for C. elegans that is constructed from loops in which different regions of the brain state space can be mapped to specific and interpretable macroscopic behaviors in the worm.

Resampling and averaging coordinates on data

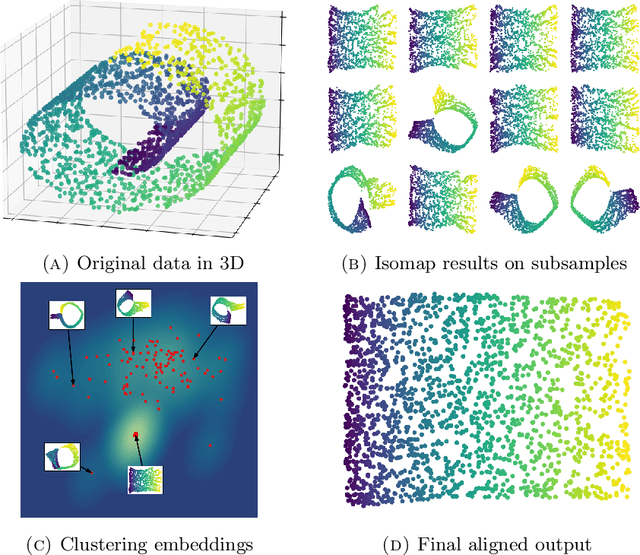
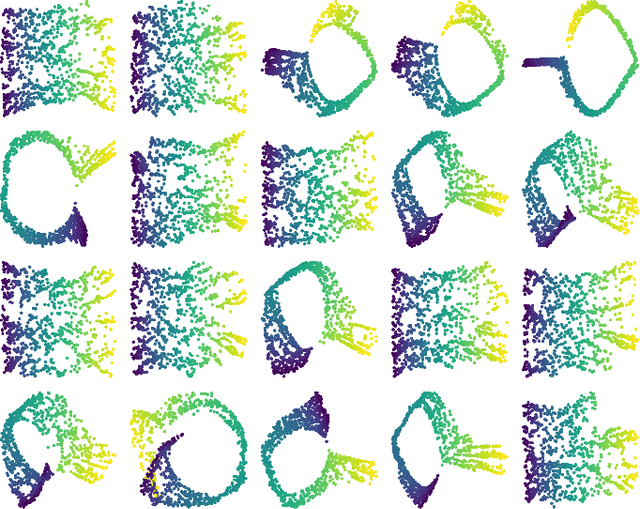
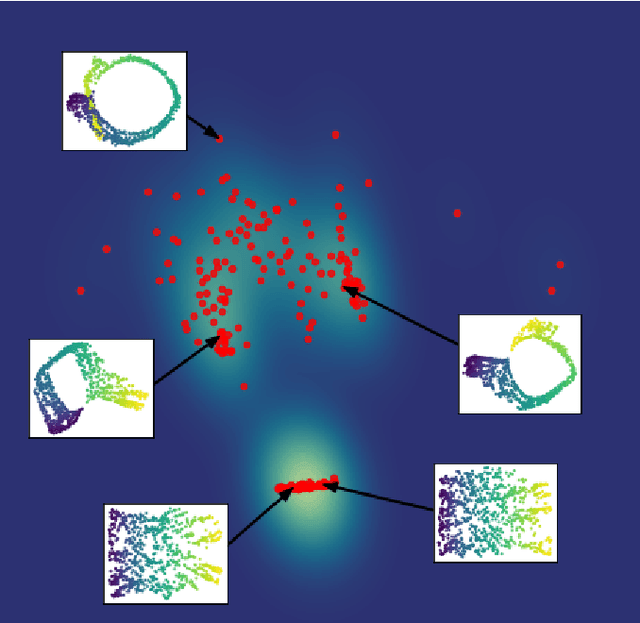
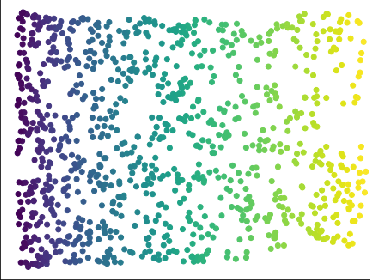
We introduce algorithms for robustly computing intrinsic coordinates on point clouds. Our approach relies on generating many candidate coordinates by subsampling the data and varying hyperparameters of the embedding algorithm (e.g., manifold learning). We then identify a subset of representative embeddings by clustering the collection of candidate coordinates and using shape descriptors from topological data analysis. The final output is the embedding obtained as an average of the representative embeddings using generalized Procrustes analysis. We validate our algorithm on both synthetic data and experimental measurements from genomics, demonstrating robustness to noise and outliers.

MREC: a fast and versatile framework for aligning and matching point clouds with applications to single cell molecular data

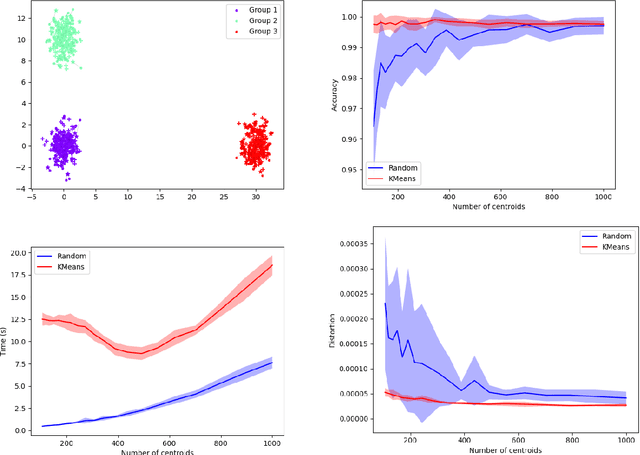
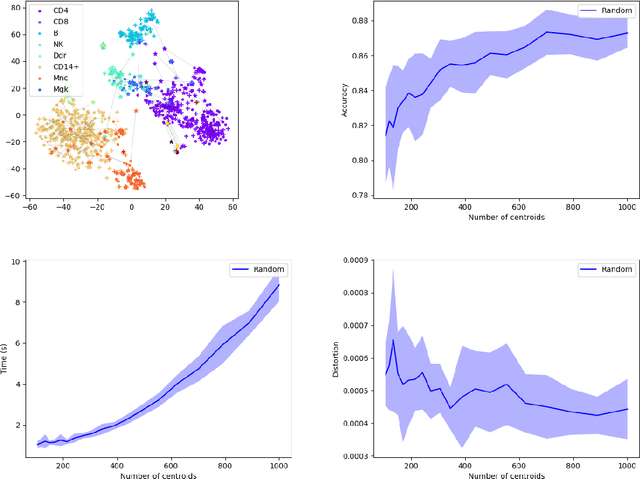
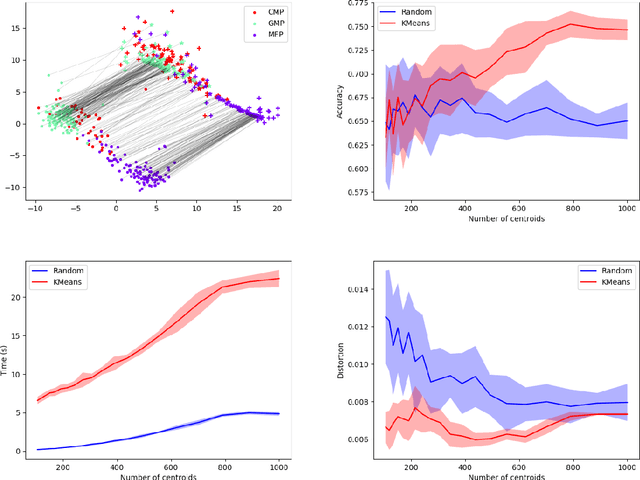
Comparing and aligning large datasets is a pervasive problem occurring across many different knowledge domains. We introduce and study MREC, a recursive decomposition algorithm for computing matchings between data sets. The basic idea is to partition the data, match the partitions, and then recursively match the points within each pair of identified partitions. The matching itself is done using black box matching procedures that are too expensive to run on the entire data set. Using an absolute measure of the quality of a matching, the framework supports optimization over parameters including partitioning procedures and matching algorithms. By design, MREC can be applied to extremely large data sets. We analyze the procedure to describe when we can expect it to work well and demonstrate its flexibility and power by applying it to a number of alignment problems arising in the analysis of single cell molecular data.