Bayesian Consistency with the Supremum Metric

We present simple conditions for Bayesian consistency in the supremum metric. The key to the technique is a triangle inequality which allows us to explicitly use weak convergence, a consequence of the standard Kullback--Leibler support condition for the prior. A further condition is to ensure that smoothed versions of densities are not too far from the original density, thus dealing with densities which could track the data too closely. A key result of the paper is that we demonstrate supremum consistency using weaker conditions compared to those currently used to secure $\mathbb{L}_1$ consistency.

On Integral Theorems: Monte Carlo Estimators and Optimal Functions

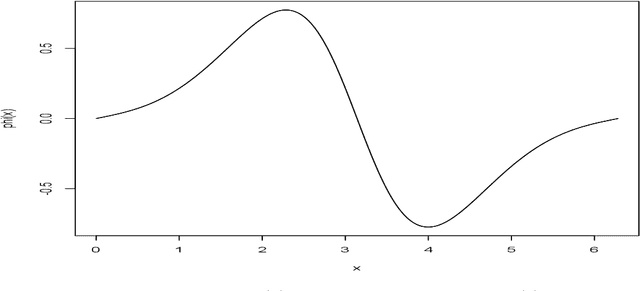
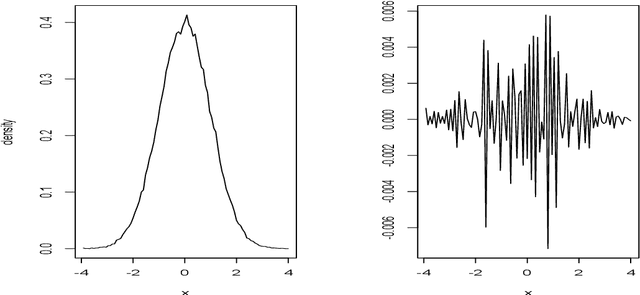
We introduce a class of integral theorems based on cyclic functions and Riemann sums approximating integrals theorem. The Fourier integral theorem, derived as a combination of a transform and inverse transform, arises as a special case. The integral theorems provide natural estimators of density functions via Monte Carlo integration. Assessments of the quality of the density estimators can be used to obtain optimal cyclic functions which minimize square integrals. Our proof techniques rely on a variational approach in ordinary differential equations and the Cauchy residue theorem in complex analysis.

Statistical Analysis from the Fourier Integral Theorem

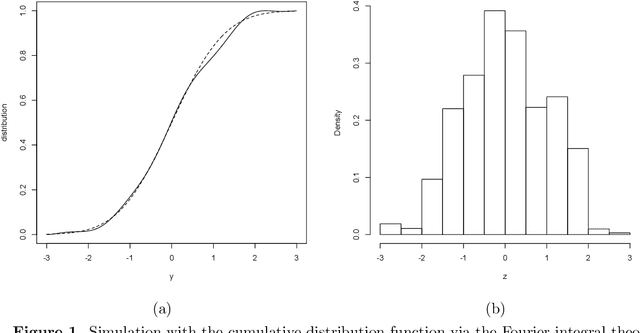
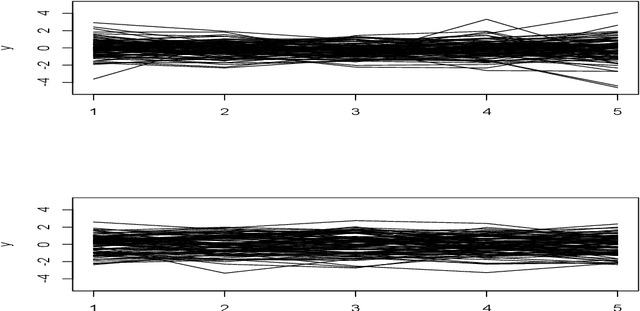
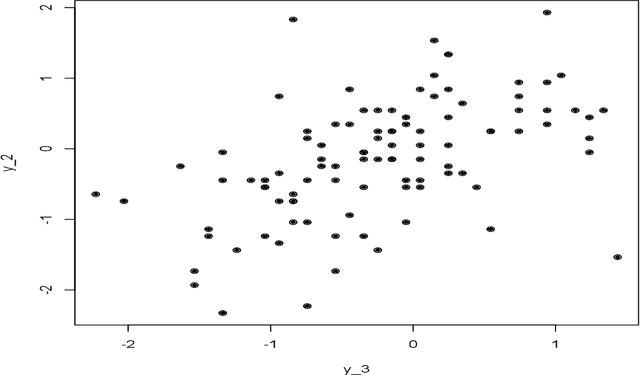
Taking the Fourier integral theorem as our starting point, in this paper we focus on natural Monte Carlo and fully nonparametric estimators of multivariate distributions and conditional distribution functions. We do this without the need for any estimated covariance matrix or dependence structure between variables. These aspects arise immediately from the integral theorem. Being able to model multivariate data sets using conditional distribution functions we can study a number of problems, such as prediction for Markov processes, estimation of mixing distribution functions which depend on covariates, and general multivariate data. Estimators are explicit Monte Carlo based and require no recursive or iterative algorithms.

A Reinforcement Learning Based Approach to Play Calling in Football

With the vast amount of data collected on football and the growth of computing abilities, many games involving decision choices can be optimized. The underlying rule is the maximization of an expected utility of outcomes and the law of large numbers. The data available allows us to compute with high accuracy the probabilities of outcomes of decisions and the well defined points system in the game allows us to have the necessary terminal utilities. With some well established theory we can then optimize choices at a single play level.

Multivariate Smoothing via the Fourier Integral Theorem and Fourier Kernel

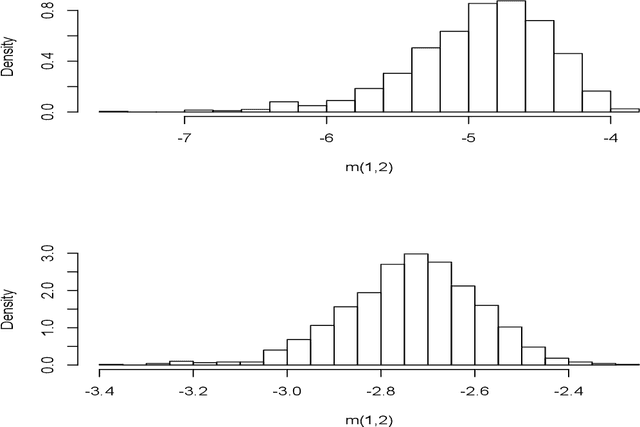
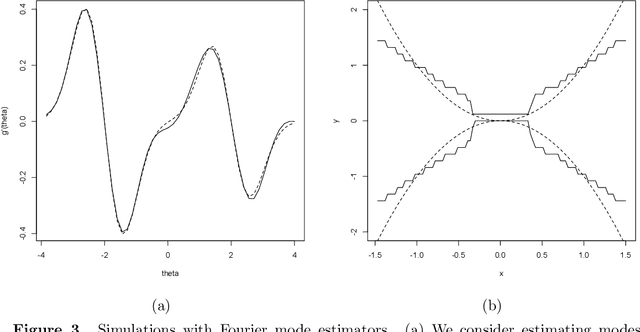
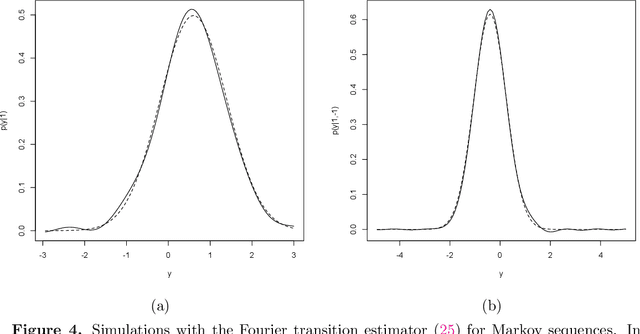
Starting with the Fourier integral theorem, we present natural Monte Carlo estimators of multivariate functions including densities, mixing densities, transition densities, regression functions, and the search for modes of multivariate density functions (modal regression). Rates of convergence are established and, in many cases, provide superior rates to current standard estimators such as those based on kernels, including kernel density estimators and kernel regression functions. Numerical illustrations are presented.

Testing to distinguish measures on metric spaces

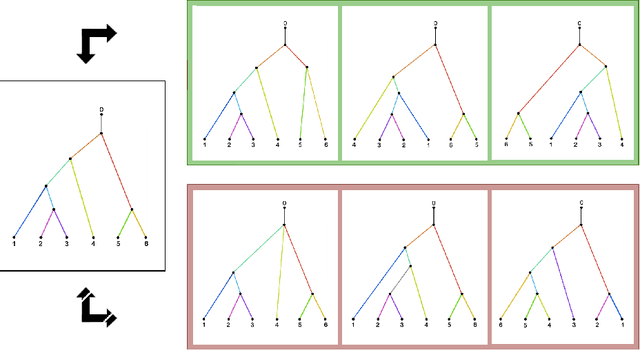
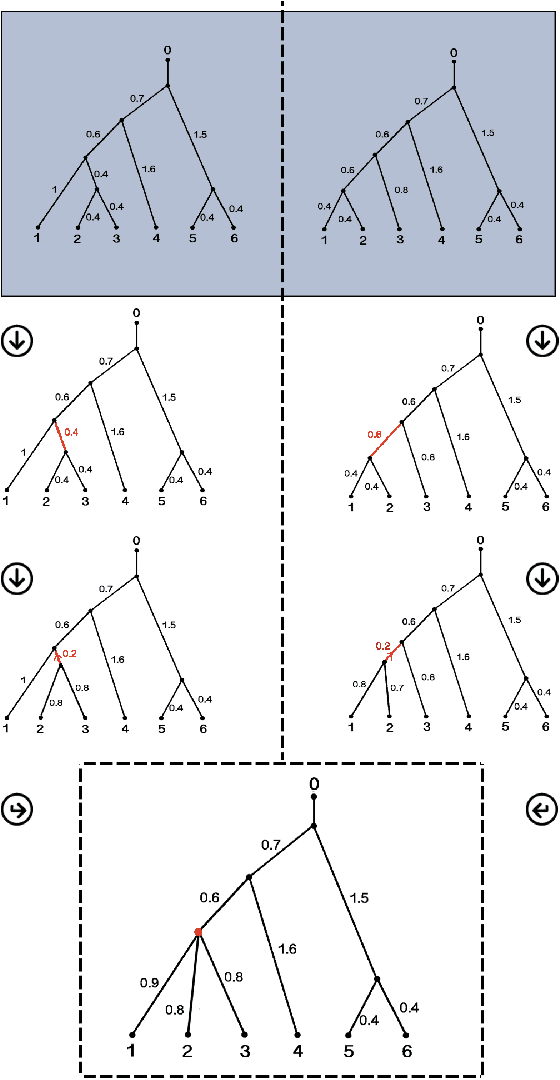
We study the problem of distinguishing between two distributions on a metric space; i.e., given metric measure spaces $({\mathbb X}, d, \mu_1)$ and $({\mathbb X}, d, \mu_2)$, we are interested in the problem of determining from finite data whether or not $\mu_1$ is $\mu_2$. The key is to use pairwise distances between observations and, employing a reconstruction theorem of Gromov, we can perform such a test using a two sample Kolmogorov--Smirnov test. A real analysis using phylogenetic trees and flu data is presented.