Selective Mixup Fine-Tuning for Optimizing Non-Decomposable Objectives

The rise in internet usage has led to the generation of massive amounts of data, resulting in the adoption of various supervised and semi-supervised machine learning algorithms, which can effectively utilize the colossal amount of data to train models. However, before deploying these models in the real world, these must be strictly evaluated on performance measures like worst-case recall and satisfy constraints such as fairness. We find that current state-of-the-art empirical techniques offer sub-optimal performance on these practical, non-decomposable performance objectives. On the other hand, the theoretical techniques necessitate training a new model from scratch for each performance objective. To bridge the gap, we propose SelMix, a selective mixup-based inexpensive fine-tuning technique for pre-trained models, to optimize for the desired objective. The core idea of our framework is to determine a sampling distribution to perform a mixup of features between samples from particular classes such that it optimizes the given objective. We comprehensively evaluate our technique against the existing empirical and theoretically principled methods on standard benchmark datasets for imbalanced classification. We find that proposed SelMix fine-tuning significantly improves the performance for various practical non-decomposable objectives across benchmarks.

Cost-Sensitive Self-Training for Optimizing Non-Decomposable Metrics

Self-training based semi-supervised learning algorithms have enabled the learning of highly accurate deep neural networks, using only a fraction of labeled data. However, the majority of work on self-training has focused on the objective of improving accuracy, whereas practical machine learning systems can have complex goals (e.g. maximizing the minimum of recall across classes, etc.) that are non-decomposable in nature. In this work, we introduce the Cost-Sensitive Self-Training (CSST) framework which generalizes the self-training-based methods for optimizing non-decomposable metrics. We prove that our framework can better optimize the desired non-decomposable metric utilizing unlabeled data, under similar data distribution assumptions made for the analysis of self-training. Using the proposed CSST framework, we obtain practical self-training methods (for both vision and NLP tasks) for optimizing different non-decomposable metrics using deep neural networks. Our results demonstrate that CSST achieves an improvement over the state-of-the-art in majority of the cases across datasets and objectives.

Fast and Multi-aspect Mining of Complex Time-stamped Event Streams

Given a huge, online stream of time-evolving events with multiple attributes, such as online shopping logs: (item, price, brand, time), and local mobility activities: (pick-up and drop-off locations, time), how can we summarize large, dynamic high-order tensor streams? How can we see any hidden patterns, rules, and anomalies? Our answer is to focus on two types of patterns, i.e., ''regimes'' and ''components'', for which we present CubeScope, an efficient and effective method over high-order tensor streams. Specifically, it identifies any sudden discontinuity and recognizes distinct dynamical patterns, ''regimes'' (e.g., weekday/weekend/holiday patterns). In each regime, it also performs multi-way summarization for all attributes (e.g., item, price, brand, and time) and discovers hidden ''components'' representing latent groups (e.g., item/brand groups) and their relationship. Thanks to its concise but effective summarization, CubeScope can also detect the sudden appearance of anomalies and identify the types of anomalies that occur in practice. Our proposed method has the following properties: (a) Effective: it captures dynamical multi-aspect patterns, i.e., regimes and components, and statistically summarizes all the events; (b) General: it is practical for successful application to data compression, pattern discovery, and anomaly detection on various types of tensor streams; (c) Scalable: our algorithm does not depend on the length of the data stream and its dimensionality. Extensive experiments on real datasets demonstrate that CubeScope finds meaningful patterns and anomalies correctly, and consistently outperforms the state-of-the-art methods as regards accuracy and execution speed.

Toward Unlimited Self-Learning Monte Carlo with Annealing Process Using VAE's Implicit Isometricity

Self-learning Monte Carlo (SLMC) methods are recently proposed to accelerate Markov chain Monte Carlo (MCMC) methods by using a machine learning model.With generative models having latent variables, SLMC methods realize efficient Monte Carlo updates with less autocorrelation. However, SLMC methods are difficult to directly apply to multimodal distributions for which training data are difficult to obtain. In this paper, we propose a novel SLMC method called the ``annealing VAE-SLMC" to drastically expand the range of applications. Our VAE-SLMC utilizes a variational autoencoder (VAE) as a generative model to make efficient parallel proposals independent of any previous state by applying the theoretically derived implicit isometricity of the VAE. We combine an adaptive annealing process to the VAE-SLMC, making our method applicable to the cases where obtaining unbiased training data is difficult in practical sense due to slow mixing. We also propose a parallel annealing process and an exchange process between chains to make the annealing operation more precise and efficient. Experiments validate that our method can proficiently obtain unbiased samples from multiple multimodal toy distributions and practical multimodal posterior distributions, which is difficult to achieve with the existing SLMC methods.

Topological Uncertainty: Monitoring trained neural networks through persistence of activation graphs

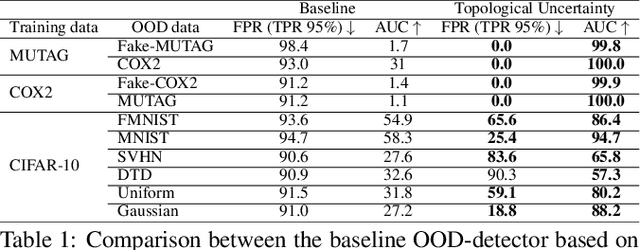
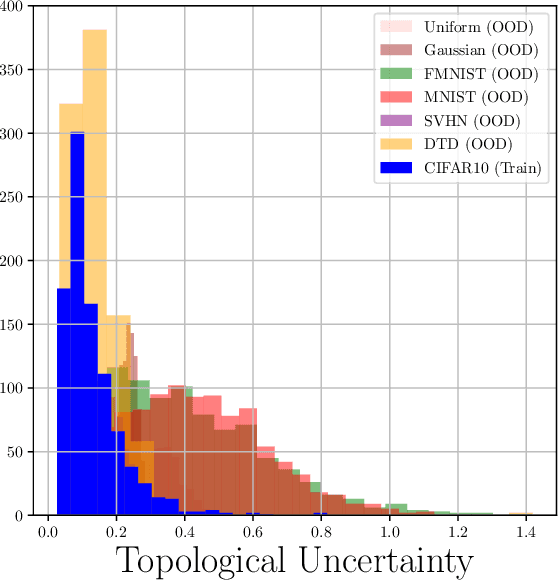
Although neural networks are capable of reaching astonishing performances on a wide variety of contexts, properly training networks on complicated tasks requires expertise and can be expensive from a computational perspective. In industrial applications, data coming from an open-world setting might widely differ from the benchmark datasets on which a network was trained. Being able to monitor the presence of such variations without retraining the network is of crucial importance. In this article, we develop a method to monitor trained neural networks based on the topological properties of their activation graphs. To each new observation, we assign a Topological Uncertainty, a score that aims to assess the reliability of the predictions by investigating the whole network instead of its final layer only, as typically done by practitioners. Our approach entirely works at a post-training level and does not require any assumption on the network architecture, optimization scheme, nor the use of data augmentation or auxiliary datasets; and can be faithfully applied on a large range of network architectures and data types. We showcase experimentally the potential of Topological Uncertainty in the context of trained network selection, Out-Of-Distribution detection, and shift-detection, both on synthetic and real datasets of images and graphs.

ATOL: Automatic Topologically-Oriented Learning

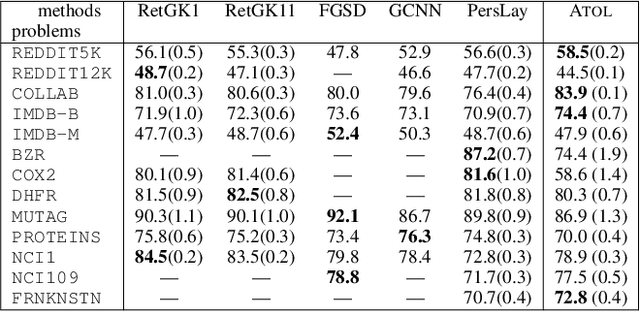
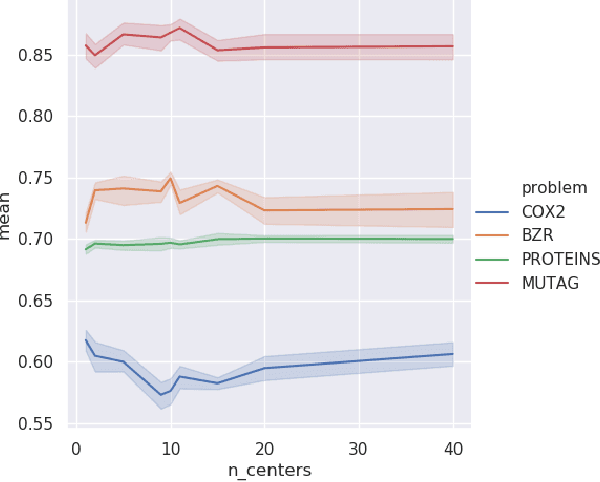
There are abundant cases for using Topological Data Analysis (TDA) in a learning context, but robust topological information commonly comes in the form of a set of persistence diagrams, objects that by nature are uneasy to affix to a generic machine learning framework. We introduce a vectorisation method for diagrams that allows to collect information from topological descriptors into a format fit for machine learning tools. Based on a few observations, the method is learned and tailored to discriminate the various important plane regions a diagram is set into. With this tool one can automatically augment any sort of machine learning problem with access to a TDA method, enhance performances, construct features reflecting underlying changes in topological behaviour. The proposed methodology comes with only high level tuning parameters such as the encoding budget for topological features. We provide an open-access, ready-to-use implementation and notebook. We showcase the strengths and versatility of our approach on a number of applications. From emulous and modern graph collections to a highly topological synthetic dynamical orbits data, we prove that the method matches or beats the state-of-the-art in encoding persistence diagrams to solve hard problems. We then apply our method in the context of an industrial, difficult time-series regression problem and show the approach to be relevant.

Topological Data Analysis for Arrhythmia Detection through Modular Neural Networks

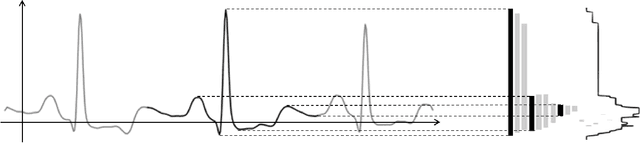
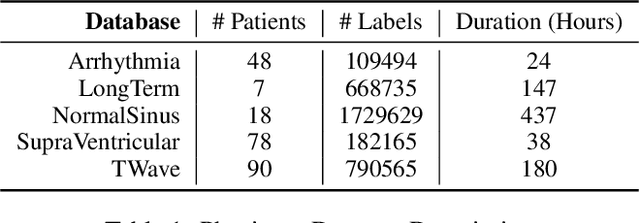
This paper presents an innovative and generic deep learning approach to monitor heart conditions from ECG signals.We focus our attention on both the detection and classification of abnormal heartbeats, known as arrhythmia. We strongly insist on generalization throughout the construction of a deep-learning model that turns out to be effective for new unseen patient. The novelty of our approach relies on the use of topological data analysis as basis of our multichannel architecture, to diminish the bias due to individual differences. We show that our structure reaches the performances of the state-of-the-art methods regarding arrhythmia detection and classification.

PersLay: A Simple and Versatile Neural Network Layer for Persistence Diagrams

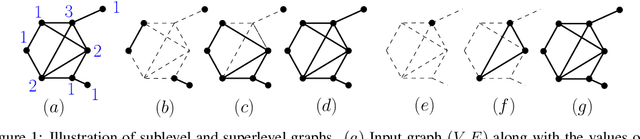
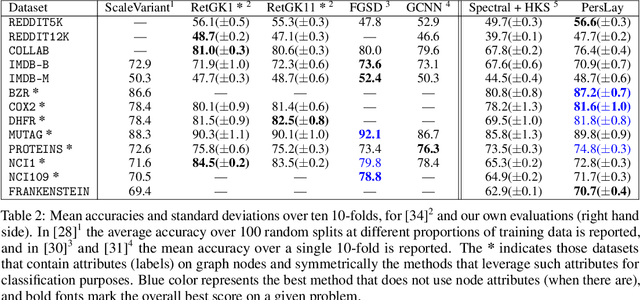
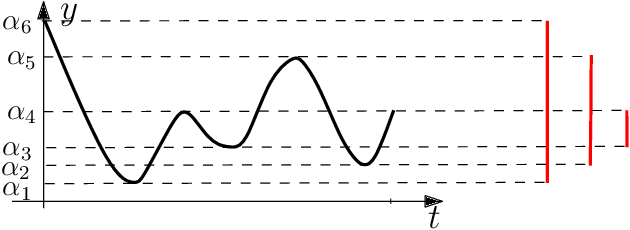
Persistence diagrams, a key descriptor from Topological Data Analysis, encode and summarize all sorts of topological features and have already proved pivotal in many different applications of data science. But persistence diagrams are weakly structured and therefore constitute a difficult input for most Machine Learning techniques. To address this concern several vectorization methods have been put forward that embed persistence diagrams into either finite-dimensional Euclidean spaces or implicit Hilbert spaces with kernels. But finite-dimensional embeddings are prone to miss a lot of information about persistence diagrams, while kernel methods require the full computation of the kernel matrix. We introduce PersLay: a simple, highly modular layer of learning architecture for persistence diagrams that allows to exploit the full capacities of neural networks on topological information from any dataset. This layer encompasses most of the vectorization methods of the literature. We illustrate its strengths on challenging classification problems on dynamical systems orbit or real-life graph data, with results improving or comparable to the state-of-the-art. In order to exploit topological information from graph data, we show how graph structures can be encoded in the so-called extended persistence diagrams computed with the heat kernel signatures of the graphs.

A General Neural Network Architecture for Persistence Diagrams and Graph Classification

Graph classification is a difficult problem that has drawn a lot of attention from the machine learning community over the past few years. This is mainly due to the fact that, contrarily to Euclidean vectors, the inherent complexity of graph structures can be quite hard to encode and handle for traditional classifiers. Even though kernels have been proposed in the literature, the increase in the dataset sizes has greatly limited the use of kernel methods since computation and storage of kernel matrices has become impracticable. In this article, we propose to use extended persistence diagrams to efficiently encode graph structure. More precisely, we show that using the so-called heat kernel signatures for the computation of these extended persistence diagrams allows one to quickly and efficiently summarize the graph structure. Then, we build on the recent development of neural networks for point clouds to define an architecture for (extended) persistence diagrams which is modular and easy-to-use. Finally, we demonstrate the usefulness of our approach by validating our architecture on several graph datasets, on which the obtained results are comparable to the state-of-the-art for graph classification.