Toward Unlimited Self-Learning Monte Carlo with Annealing Process Using VAE's Implicit Isometricity

Self-learning Monte Carlo (SLMC) methods are recently proposed to accelerate Markov chain Monte Carlo (MCMC) methods by using a machine learning model.With generative models having latent variables, SLMC methods realize efficient Monte Carlo updates with less autocorrelation. However, SLMC methods are difficult to directly apply to multimodal distributions for which training data are difficult to obtain. In this paper, we propose a novel SLMC method called the ``annealing VAE-SLMC" to drastically expand the range of applications. Our VAE-SLMC utilizes a variational autoencoder (VAE) as a generative model to make efficient parallel proposals independent of any previous state by applying the theoretically derived implicit isometricity of the VAE. We combine an adaptive annealing process to the VAE-SLMC, making our method applicable to the cases where obtaining unbiased training data is difficult in practical sense due to slow mixing. We also propose a parallel annealing process and an exchange process between chains to make the annealing operation more precise and efficient. Experiments validate that our method can proficiently obtain unbiased samples from multiple multimodal toy distributions and practical multimodal posterior distributions, which is difficult to achieve with the existing SLMC methods.

Quantitative Understanding of VAE by Interpreting ELBO as Rate Distortion Cost of Transform Coding

VAE (Variational autoencoder) estimates the posterior parameters (mean and variance) of latent variables corresponding to each input data. While it is used for many tasks, the transparency of the model is still an underlying issue. This paper provides a quantitative understanding of VAE property by interpreting ELBO maximization as Rate-distortion optimization of transform coding. According to the Rate-distortion theory, the optimal transform coding is achieved by using PCA-like orthonormal (orthogonal and unit norm) transform. From this analogy, we show theoretically and experimentally that VAE can be mapped to an implicit orthonormal transform with a scale factor derived from the posterior parameter. As a result, the quantitative importance of each latent variable can be evaluated like the eigenvalue of PCA. We can also estimate the data probabilities in the input space from the prior, loss metrics, and corresponding posterior parameters.

Rate-Distortion Optimization Guided Autoencoder for Generative Approach with quantitatively measurable latent space

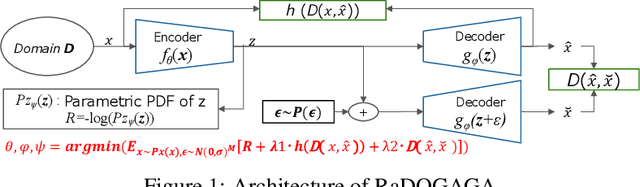
In the generative model approach of machine learning, it is essential to acquire an accurate probabilistic model and compress the dimension of data for easy treatment. However, in the conventional deep-autoencoder based generative model such as VAE, the probability of the real space cannot be obtained correctly from that of in the latent space, because the scaling between both spaces is not controlled. This has also been an obstacle to quantifying the impact of the variation of latent variables on data. In this paper, we propose Rate-Distortion Optimization guided autoencoder, in which the Jacobi matrix from real space to latent space has orthonormality. It is proved theoretically and experimentally that (i) the probability distribution of the latent space obtained by this model is proportional to the probability distribution of the real space because Jacobian between two spaces is constant; (ii) our model behaves as non-linear PCA, where energy of acquired latent space is concentrated on several principal components and the influence of each component can be evaluated quantitatively. Furthermore, to verify the usefulness on the practical application, we evaluate its performance in unsupervised anomaly detection and it outperforms current state-of-the-art methods.