RipsNet: a general architecture for fast and robust estimation of the persistent homology of point clouds

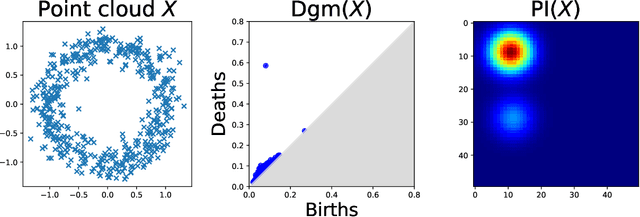
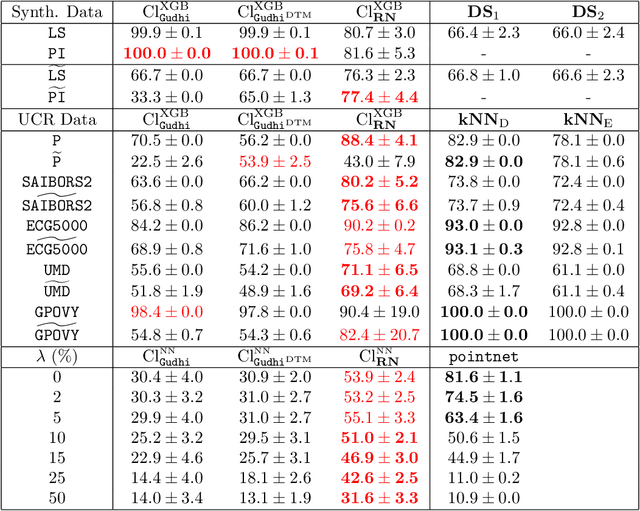
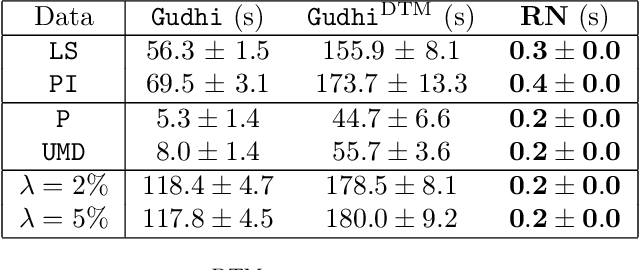
The use of topological descriptors in modern machine learning applications, such as Persistence Diagrams (PDs) arising from Topological Data Analysis (TDA), has shown great potential in various domains. However, their practical use in applications is often hindered by two major limitations: the computational complexity required to compute such descriptors exactly, and their sensitivity to even low-level proportions of outliers. In this work, we propose to bypass these two burdens in a data-driven setting by entrusting the estimation of (vectorization of) PDs built on top of point clouds to a neural network architecture that we call RipsNet. Once trained on a given data set, RipsNet can estimate topological descriptors on test data very efficiently with generalization capacity. Furthermore, we prove that RipsNet is robust to input perturbations in terms of the 1-Wasserstein distance, a major improvement over the standard computation of PDs that only enjoys Hausdorff stability, yielding RipsNet to substantially outperform exactly-computed PDs in noisy settings. We showcase the use of RipsNet on both synthetic and real-world data. Our open-source implementation is publicly available at https://github.com/hensel-f/ripsnet and will be included in the Gudhi library.

Topological Uncertainty: Monitoring trained neural networks through persistence of activation graphs

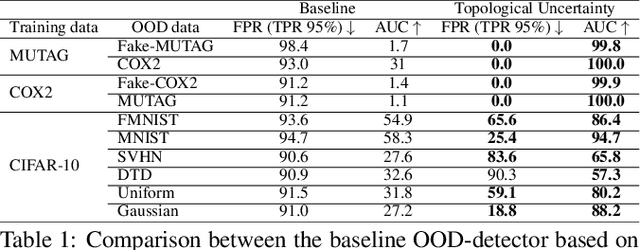
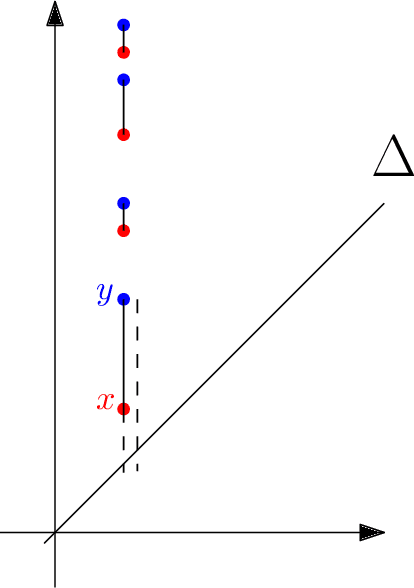
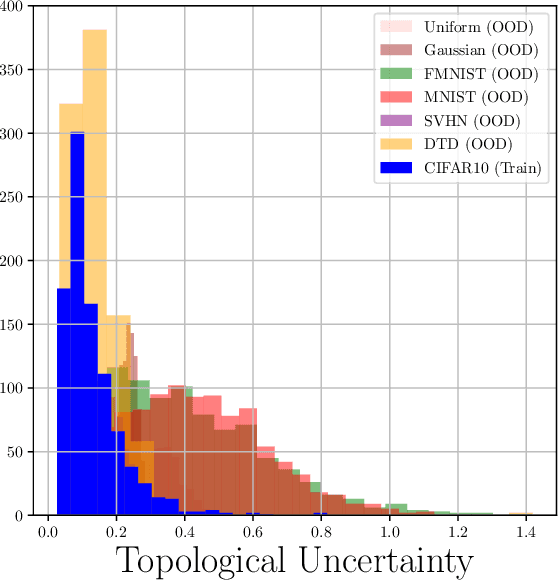
Although neural networks are capable of reaching astonishing performances on a wide variety of contexts, properly training networks on complicated tasks requires expertise and can be expensive from a computational perspective. In industrial applications, data coming from an open-world setting might widely differ from the benchmark datasets on which a network was trained. Being able to monitor the presence of such variations without retraining the network is of crucial importance. In this article, we develop a method to monitor trained neural networks based on the topological properties of their activation graphs. To each new observation, we assign a Topological Uncertainty, a score that aims to assess the reliability of the predictions by investigating the whole network instead of its final layer only, as typically done by practitioners. Our approach entirely works at a post-training level and does not require any assumption on the network architecture, optimization scheme, nor the use of data augmentation or auxiliary datasets; and can be faithfully applied on a large range of network architectures and data types. We showcase experimentally the potential of Topological Uncertainty in the context of trained network selection, Out-Of-Distribution detection, and shift-detection, both on synthetic and real datasets of images and graphs.

Optimal rates of convergence for persistence diagrams in Topological Data Analysis

Computational topology has recently known an important development toward data analysis, giving birth to the field of topological data analysis. Topological persistence, or persistent homology, appears as a fundamental tool in this field. In this paper, we study topological persistence in general metric spaces, with a statistical approach. We show that the use of persistent homology can be naturally considered in general statistical frameworks and persistence diagrams can be used as statistics with interesting convergence properties. Some numerical experiments are performed in various contexts to illustrate our results.