MAGDiff: Covariate Data Set Shift Detection via Activation Graphs of Deep Neural Networks

Despite their successful application to a variety of tasks, neural networks remain limited, like other machine learning methods, by their sensitivity to shifts in the data: their performance can be severely impacted by differences in distribution between the data on which they were trained and that on which they are deployed. In this article, we propose a new family of representations, called MAGDiff, that we extract from any given neural network classifier and that allows for efficient covariate data shift detection without the need to train a new model dedicated to this task. These representations are computed by comparing the activation graphs of the neural network for samples belonging to the training distribution and to the target distribution, and yield powerful data- and task-adapted statistics for the two-sample tests commonly used for data set shift detection. We demonstrate this empirically by measuring the statistical powers of two-sample Kolmogorov-Smirnov (KS) tests on several different data sets and shift types, and showing that our novel representations induce significant improvements over a state-of-the-art baseline relying on the network output.

RipsNet: a general architecture for fast and robust estimation of the persistent homology of point clouds

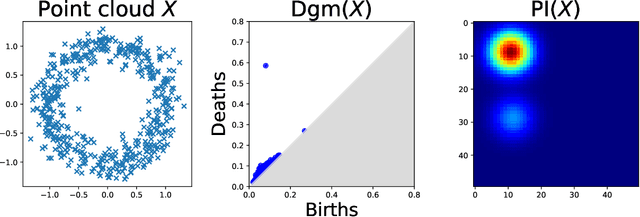
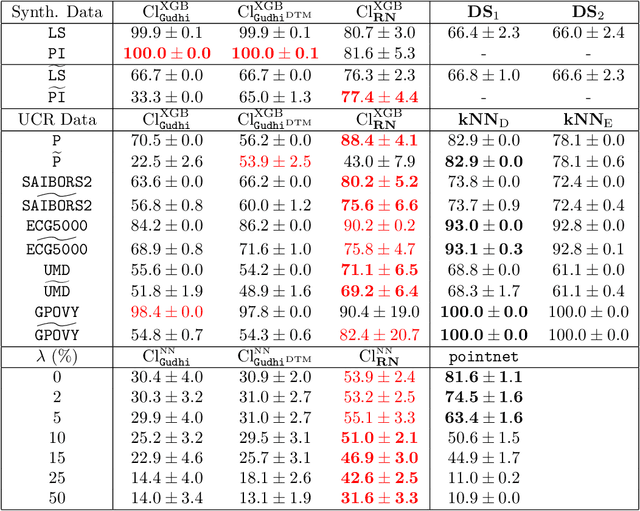
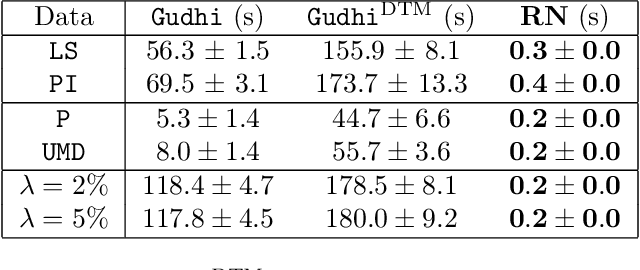
The use of topological descriptors in modern machine learning applications, such as Persistence Diagrams (PDs) arising from Topological Data Analysis (TDA), has shown great potential in various domains. However, their practical use in applications is often hindered by two major limitations: the computational complexity required to compute such descriptors exactly, and their sensitivity to even low-level proportions of outliers. In this work, we propose to bypass these two burdens in a data-driven setting by entrusting the estimation of (vectorization of) PDs built on top of point clouds to a neural network architecture that we call RipsNet. Once trained on a given data set, RipsNet can estimate topological descriptors on test data very efficiently with generalization capacity. Furthermore, we prove that RipsNet is robust to input perturbations in terms of the 1-Wasserstein distance, a major improvement over the standard computation of PDs that only enjoys Hausdorff stability, yielding RipsNet to substantially outperform exactly-computed PDs in noisy settings. We showcase the use of RipsNet on both synthetic and real-world data. Our open-source implementation is publicly available at https://github.com/hensel-f/ripsnet and will be included in the Gudhi library.