Graph Community Augmentation with GMM-based Modeling in Latent Space
Paper and Code
Dec 02, 2024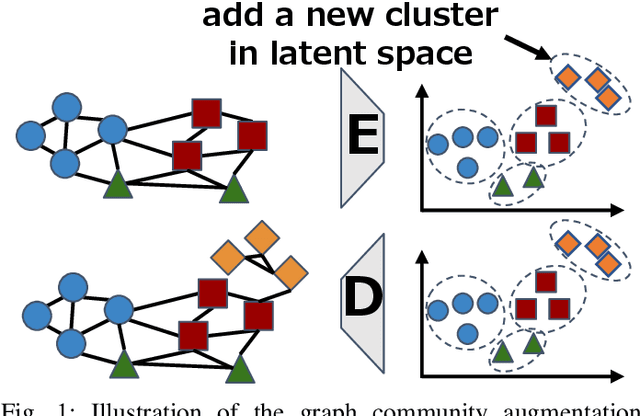
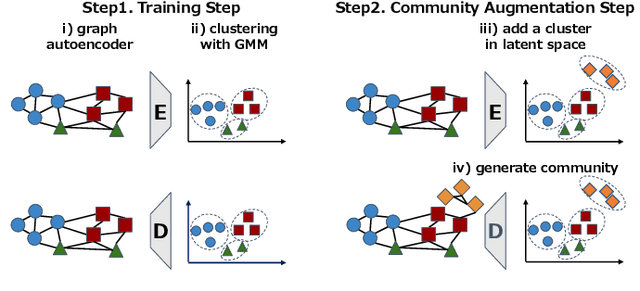
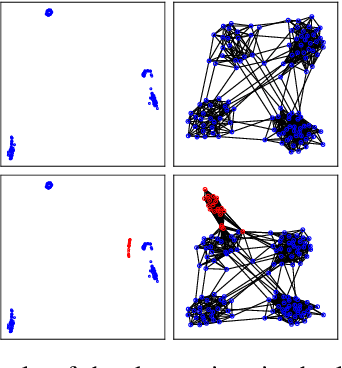
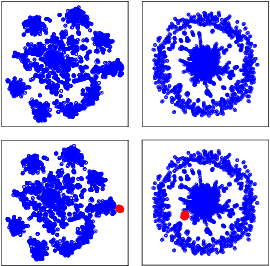
This study addresses the issue of graph generation with generative models. In particular, we are concerned with graph community augmentation problem, which refers to the problem of generating unseen or unfamiliar graphs with a new community out of the probability distribution estimated with a given graph dataset. The graph community augmentation means that the generated graphs have a new community. There is a chance of discovering an unseen but important structure of graphs with a new community, for example, in a social network such as a purchaser network. Graph community augmentation may also be helpful for generalization of data mining models in a case where it is difficult to collect real graph data enough. In fact, there are many ways to generate a new community in an existing graph. It is desirable to discover a new graph with a new community beyond the given graph while we keep the structure of the original graphs to some extent for the generated graphs to be realistic. To this end, we propose an algorithm called the graph community augmentation (GCA). The key ideas of GCA are (i) to fit Gaussian mixture model (GMM) to data points in the latent space into which the nodes in the original graph are embedded, and (ii) to add data points in the new cluster in the latent space for generating a new community based on the minimum description length (MDL) principle. We empirically demonstrate the effectiveness of GCA for generating graphs with a new community structure on synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge