Balancing Summarization and Change Detection in Graph Streams
Paper and Code
Nov 30, 2023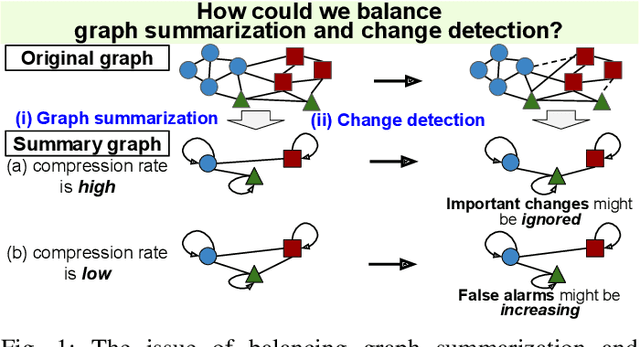
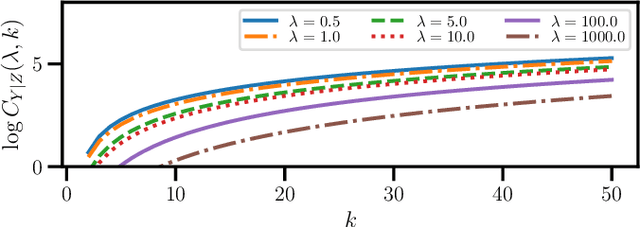
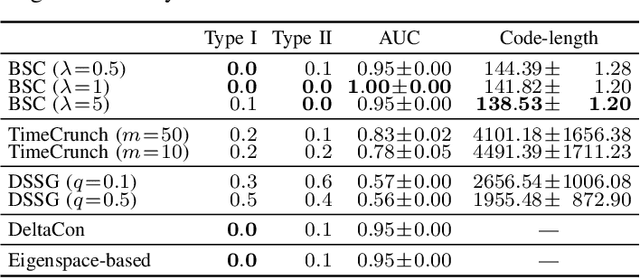

This study addresses the issue of balancing graph summarization and graph change detection. Graph summarization compresses large-scale graphs into a smaller scale. However, the question remains: To what extent should the original graph be compressed? This problem is solved from the perspective of graph change detection, aiming to detect statistically significant changes using a stream of summary graphs. If the compression rate is extremely high, important changes can be ignored, whereas if the compression rate is extremely low, false alarms may increase with more memory. This implies that there is a trade-off between compression rate in graph summarization and accuracy in change detection. We propose a novel quantitative methodology to balance this trade-off to simultaneously realize reliable graph summarization and change detection. We introduce a probabilistic structure of hierarchical latent variable model into a graph, thereby designing a parameterized summary graph on the basis of the minimum description length principle. The parameter specifying the summary graph is then optimized so that the accuracy of change detection is guaranteed to suppress Type I error probability (probability of raising false alarms) to be less than a given confidence level. First, we provide a theoretical framework for connecting graph summarization with change detection. Then, we empirically demonstrate its effectiveness on synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge