Seiya Tokui
When Does Metadata Conditioning (NOT) Work for Language Model Pre-Training? A Study with Context-Free Grammars
Apr 24, 2025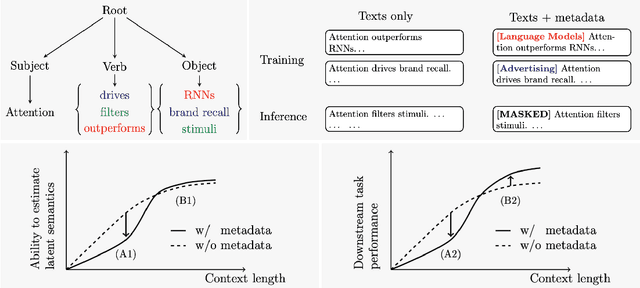
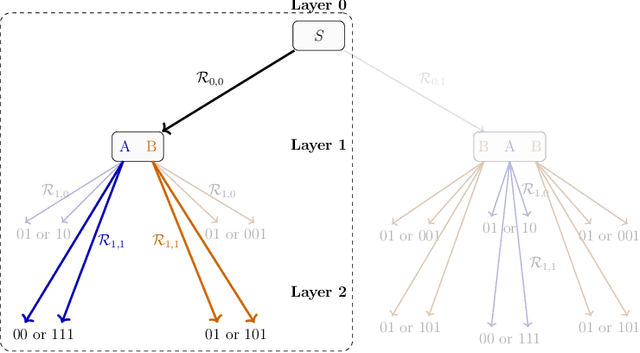
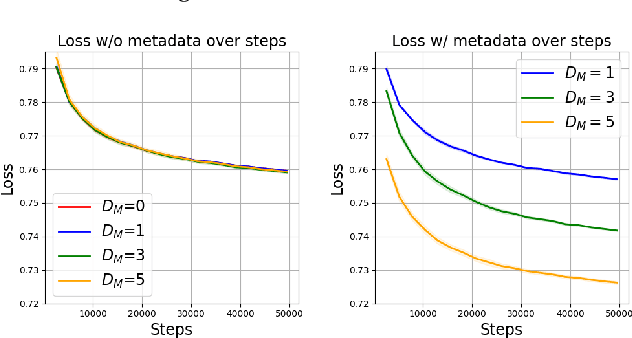

Abstract:The ability to acquire latent semantics is one of the key properties that determines the performance of language models. One convenient approach to invoke this ability is to prepend metadata (e.g. URLs, domains, and styles) at the beginning of texts in the pre-training data, making it easier for the model to access latent semantics before observing the entire text. Previous studies have reported that this technique actually improves the performance of trained models in downstream tasks; however, this improvement has been observed only in specific downstream tasks, without consistent enhancement in average next-token prediction loss. To understand this phenomenon, we closely investigate how prepending metadata during pre-training affects model performance by examining its behavior using artificial data. Interestingly, we found that this approach produces both positive and negative effects on the downstream tasks. We demonstrate that the effectiveness of the approach depends on whether latent semantics can be inferred from the downstream task's prompt. Specifically, through investigations using data generated by probabilistic context-free grammars, we show that training with metadata helps improve model's performance when the given context is long enough to infer the latent semantics. In contrast, the technique negatively impacts performance when the context lacks the necessary information to make an accurate posterior inference.
Disentanglement Analysis with Partial Information Decomposition
Aug 31, 2021



Abstract:Given data generated from multiple factors of variation that cooperatively transform their appearance, disentangled representations aim at reversing the process by mapping data to multiple random variables that individually capture distinct generative factors. As the concept is intuitive but abstract, one needs to quantify it with disentanglement metrics to evaluate and compare the quality of disentangled representations between different models. Current disentanglement metrics are designed to measure the concentration, e.g., absolute deviation, variance, or entropy, of each variable conditioned by each generative factor, optionally offset by the concentration of its marginal distribution, and compare it among different variables. When representations consist of more than two variables, such metrics may fail to detect the interplay between them as they only measure pairwise interactions. In this work, we use the Partial Information Decomposition framework to evaluate information sharing between more than two variables, and build a framework, including a new disentanglement metric, for analyzing how the representations encode the generative factors distinctly, redundantly, and cooperatively. We establish an experimental protocol to assess how each metric evaluates increasingly entangled representations and confirm through artificial and realistic settings that the proposed metric correctly responds to entanglement. Our results are expected to promote information theoretic understanding of disentanglement and lead to further development of metrics as well as learning methods.
Chainer: A Deep Learning Framework for Accelerating the Research Cycle
Aug 01, 2019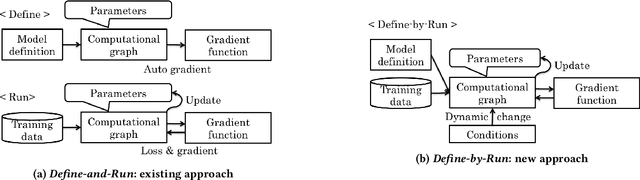
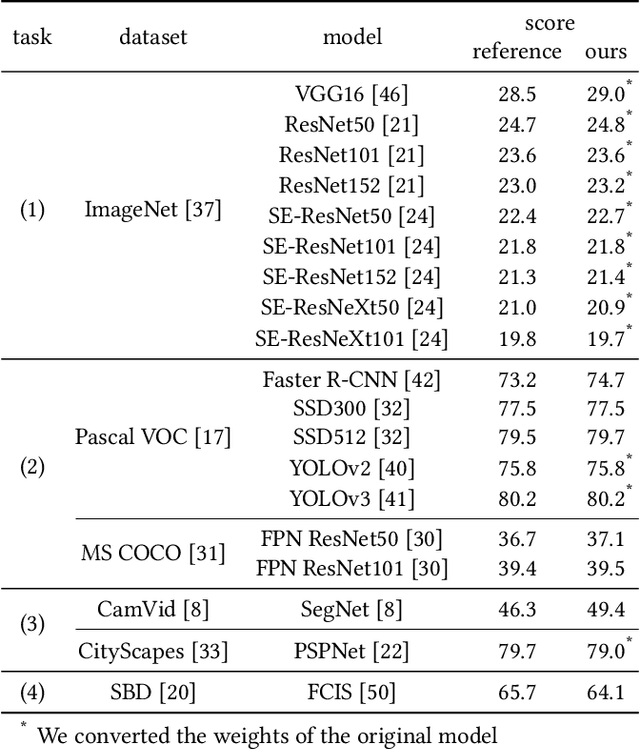


Abstract:Software frameworks for neural networks play a key role in the development and application of deep learning methods. In this paper, we introduce the Chainer framework, which intends to provide a flexible, intuitive, and high performance means of implementing the full range of deep learning models needed by researchers and practitioners. Chainer provides acceleration using Graphics Processing Units with a familiar NumPy-like API through CuPy, supports general and dynamic models in Python through Define-by-Run, and also provides add-on packages for state-of-the-art computer vision models as well as distributed training.
Adversarial Attacks and Defences Competition
Mar 31, 2018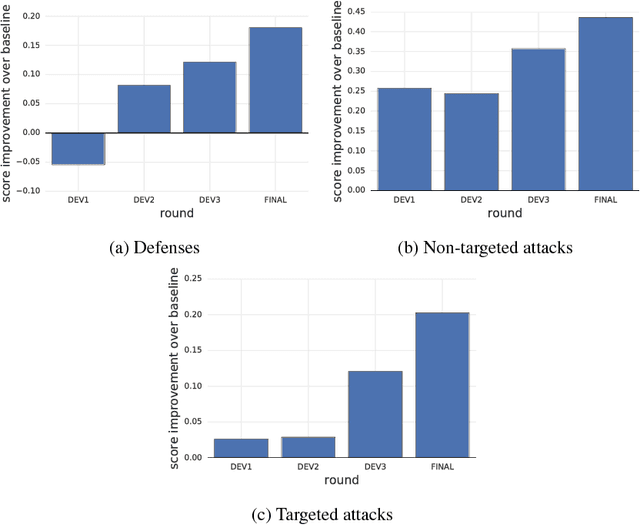
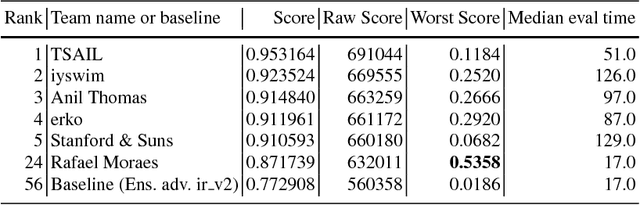
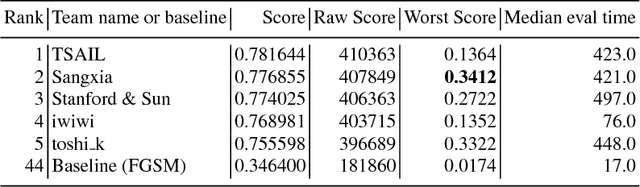
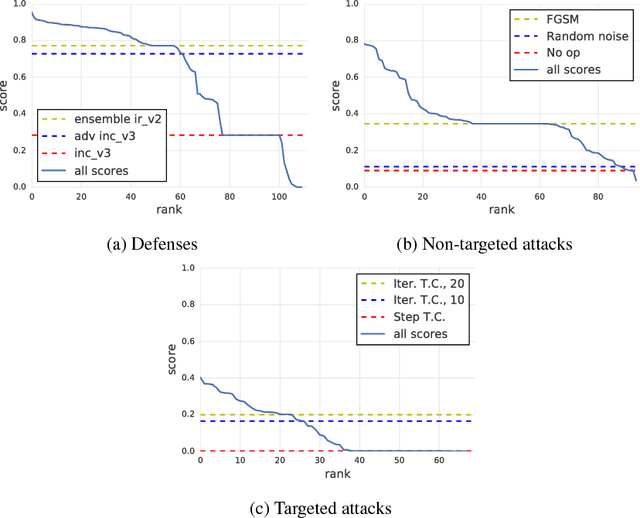
Abstract:To accelerate research on adversarial examples and robustness of machine learning classifiers, Google Brain organized a NIPS 2017 competition that encouraged researchers to develop new methods to generate adversarial examples as well as to develop new ways to defend against them. In this chapter, we describe the structure and organization of the competition and the solutions developed by several of the top-placing teams.
Learning Discrete Representations via Information Maximizing Self-Augmented Training
Jun 14, 2017



Abstract:Learning discrete representations of data is a central machine learning task because of the compactness of the representations and ease of interpretation. The task includes clustering and hash learning as special cases. Deep neural networks are promising to be used because they can model the non-linearity of data and scale to large datasets. However, their model complexity is huge, and therefore, we need to carefully regularize the networks in order to learn useful representations that exhibit intended invariance for applications of interest. To this end, we propose a method called Information Maximizing Self-Augmented Training (IMSAT). In IMSAT, we use data augmentation to impose the invariance on discrete representations. More specifically, we encourage the predicted representations of augmented data points to be close to those of the original data points in an end-to-end fashion. At the same time, we maximize the information-theoretic dependency between data and their predicted discrete representations. Extensive experiments on benchmark datasets show that IMSAT produces state-of-the-art results for both clustering and unsupervised hash learning.
Reparameterization trick for discrete variables
Nov 04, 2016

Abstract:Low-variance gradient estimation is crucial for learning directed graphical models parameterized by neural networks, where the reparameterization trick is widely used for those with continuous variables. While this technique gives low-variance gradient estimates, it has not been directly applicable to discrete variables, the sampling of which inherently requires discontinuous operations. We argue that the discontinuity can be bypassed by marginalizing out the variable of interest, which results in a new reparameterization trick for discrete variables. This reparameterization greatly reduces the variance, which is understood by regarding the method as an application of common random numbers to the estimation. The resulting estimator is theoretically guaranteed to have a variance not larger than that of the likelihood-ratio method with the optimal input-dependent baseline. We give empirical results for variational learning of sigmoid belief networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge