Universal approximation property of invertible neural networks

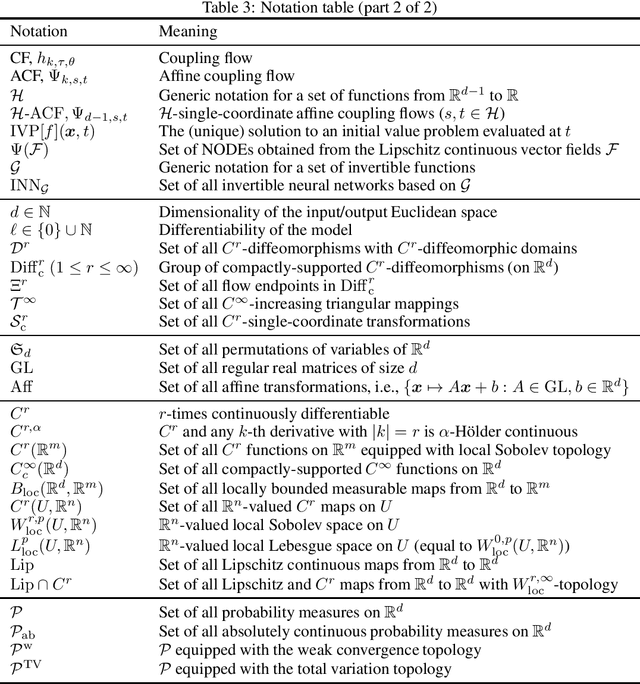
Invertible neural networks (INNs) are neural network architectures with invertibility by design. Thanks to their invertibility and the tractability of Jacobian, INNs have various machine learning applications such as probabilistic modeling, generative modeling, and representation learning. However, their attractive properties often come at the cost of restricting the layer designs, which poses a question on their representation power: can we use these models to approximate sufficiently diverse functions? To answer this question, we have developed a general theoretical framework to investigate the representation power of INNs, building on a structure theorem of differential geometry. The framework simplifies the approximation problem of diffeomorphisms, which enables us to show the universal approximation properties of INNs. We apply the framework to two representative classes of INNs, namely Coupling-Flow-based INNs (CF-INNs) and Neural Ordinary Differential Equations (NODEs), and elucidate their high representation power despite the restrictions on their architectures.

Universal Approximation Property of Neural Ordinary Differential Equations

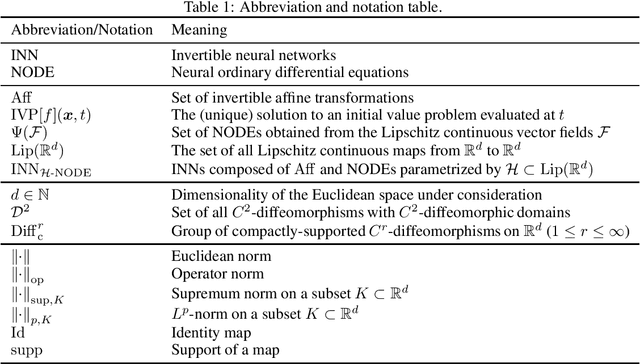
Neural ordinary differential equations (NODEs) is an invertible neural network architecture promising for its free-form Jacobian and the availability of a tractable Jacobian determinant estimator. Recently, the representation power of NODEs has been partly uncovered: they form an $L^p$-universal approximator for continuous maps under certain conditions. However, the $L^p$-universality may fail to guarantee an approximation for the entire input domain as it may still hold even if the approximator largely differs from the target function on a small region of the input space. To further uncover the potential of NODEs, we show their stronger approximation property, namely the $\sup$-universality for approximating a large class of diffeomorphisms. It is shown by leveraging a structure theorem of the diffeomorphism group, and the result complements the existing literature by establishing a fairly large set of mappings that NODEs can approximate with a stronger guarantee.

Coupling-based Invertible Neural Networks Are Universal Diffeomorphism Approximators

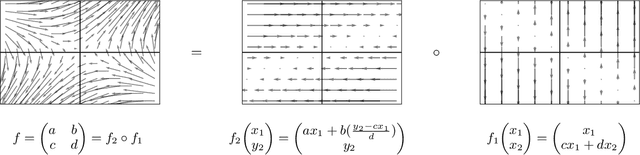
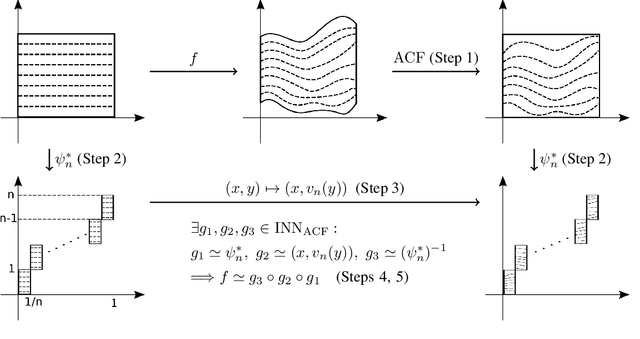
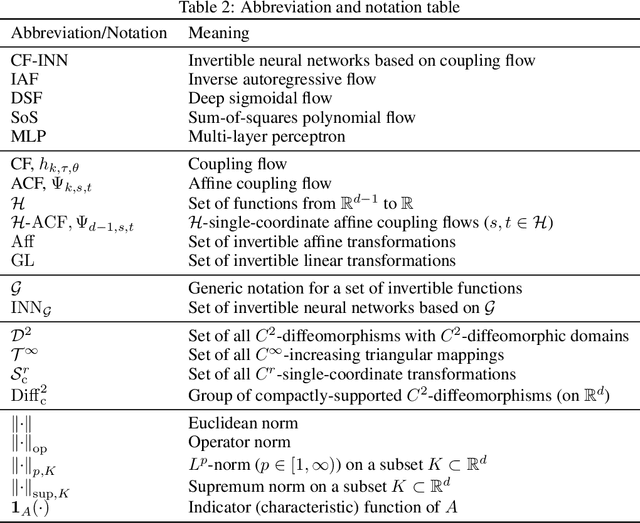
Invertible neural networks based on coupling flows (CF-INNs) have various machine learning applications such as image synthesis and representation learning. However, their desirable characteristics such as analytic invertibility come at the cost of restricting the functional forms. This poses a question on their representation power: are CF-INNs universal approximators for invertible functions? Without a universality, there could be a well-behaved invertible transformation that the CF-INN can never approximate, hence it would render the model class unreliable. We answer this question by showing a convenient criterion: a CF-INN is universal if its layers contain affine coupling and invertible linear functions as special cases. As its corollary, we can affirmatively resolve a previously unsolved problem: whether normalizing flow models based on affine coupling can be universal distributional approximators. In the course of proving the universality, we prove a general theorem to show the equivalence of the universality for certain diffeomorphism classes, a theoretical insight that is of interest by itself.

On a method to construct exponential families by representation theory

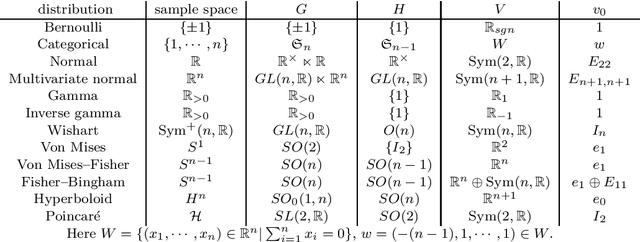
Exponential family plays an important role in information geometry. In arXiv:1811.01394, we introduced a method to construct an exponential family $\mathcal{P}=\{p_\theta\}_{\theta\in\Theta}$ on a homogeneous space $G/H$ from a pair $(V,v_0)$. Here $V$ is a representation of $G$ and $v_0$ is an $H$-fixed vector in $V$. Then the following questions naturally arise: (Q1) when is the correspondence $\theta\mapsto p_\theta$ injective? (Q2) when do distinct pairs $(V,v_0)$ and $(V',v_0')$ generate the same family? In this paper, we answer these two questions (Theorems 1 and 2). Moreover, in Section 3, we consider the case $(G,H)=(\mathbb{R}_{>0}, \{1\})$ with a certain representation on $\mathbb{R}^2$. Then we see the family obtained by our method is essentially generalized inverse Gaussian distribution (GIG).

A method to construct exponential families by representation theory

In this paper, we give a method to construct "good" exponential families systematically by representation theory. More precisely, we consider a homogeneous space $G/H$ as a sample space and construct a exponential family invariant under the transformation group $G$ by using a representation of $G$. The method generates widely used exponential families such as normal, gamma, Bernoulli, categorical, Wishart, von Mises and Fisher-Bingham distributions. Moreover, we obtain a new family of distributions on the upper half plane compatible with the Poincar\'e metric.