On a method to construct exponential families by representation theory
Paper and Code
Jul 06, 2019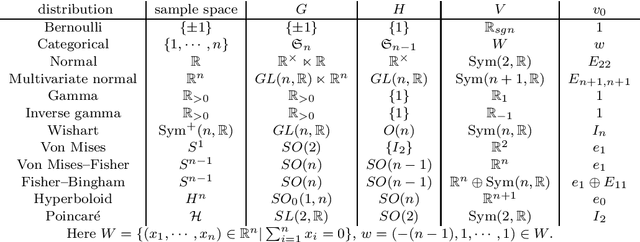
Exponential family plays an important role in information geometry. In arXiv:1811.01394, we introduced a method to construct an exponential family $\mathcal{P}=\{p_\theta\}_{\theta\in\Theta}$ on a homogeneous space $G/H$ from a pair $(V,v_0)$. Here $V$ is a representation of $G$ and $v_0$ is an $H$-fixed vector in $V$. Then the following questions naturally arise: (Q1) when is the correspondence $\theta\mapsto p_\theta$ injective? (Q2) when do distinct pairs $(V,v_0)$ and $(V',v_0')$ generate the same family? In this paper, we answer these two questions (Theorems 1 and 2). Moreover, in Section 3, we consider the case $(G,H)=(\mathbb{R}_{>0}, \{1\})$ with a certain representation on $\mathbb{R}^2$. Then we see the family obtained by our method is essentially generalized inverse Gaussian distribution (GIG).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge