On a method to construct exponential families by representation theory

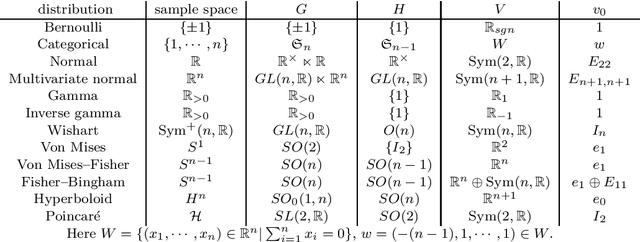
Exponential family plays an important role in information geometry. In arXiv:1811.01394, we introduced a method to construct an exponential family $\mathcal{P}=\{p_\theta\}_{\theta\in\Theta}$ on a homogeneous space $G/H$ from a pair $(V,v_0)$. Here $V$ is a representation of $G$ and $v_0$ is an $H$-fixed vector in $V$. Then the following questions naturally arise: (Q1) when is the correspondence $\theta\mapsto p_\theta$ injective? (Q2) when do distinct pairs $(V,v_0)$ and $(V',v_0')$ generate the same family? In this paper, we answer these two questions (Theorems 1 and 2). Moreover, in Section 3, we consider the case $(G,H)=(\mathbb{R}_{>0}, \{1\})$ with a certain representation on $\mathbb{R}^2$. Then we see the family obtained by our method is essentially generalized inverse Gaussian distribution (GIG).

A method to construct exponential families by representation theory

In this paper, we give a method to construct "good" exponential families systematically by representation theory. More precisely, we consider a homogeneous space $G/H$ as a sample space and construct a exponential family invariant under the transformation group $G$ by using a representation of $G$. The method generates widely used exponential families such as normal, gamma, Bernoulli, categorical, Wishart, von Mises and Fisher-Bingham distributions. Moreover, we obtain a new family of distributions on the upper half plane compatible with the Poincar\'e metric.