A method to construct exponential families by representation theory

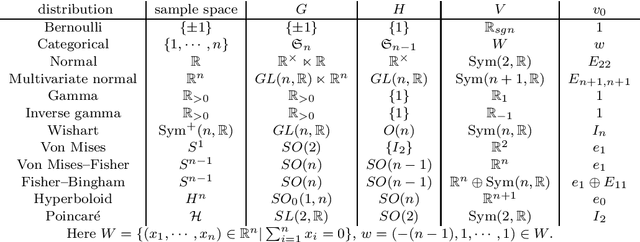
In this paper, we give a method to construct "good" exponential families systematically by representation theory. More precisely, we consider a homogeneous space $G/H$ as a sample space and construct a exponential family invariant under the transformation group $G$ by using a representation of $G$. The method generates widely used exponential families such as normal, gamma, Bernoulli, categorical, Wishart, von Mises and Fisher-Bingham distributions. Moreover, we obtain a new family of distributions on the upper half plane compatible with the Poincar\'e metric.