Generalizing Importance Weighting to A Universal Solver for Distribution Shift Problems

Distribution shift (DS) may have two levels: the distribution itself changes, and the support (i.e., the set where the probability density is non-zero) also changes. When considering the support change between the training and test distributions, there can be four cases: (i) they exactly match; (ii) the training support is wider (and thus covers the test support); (iii) the test support is wider; (iv) they partially overlap. Existing methods are good at cases (i) and (ii), while cases (iii) and (iv) are more common nowadays but still under-explored. In this paper, we generalize importance weighting (IW), a golden solver for cases (i) and (ii), to a universal solver for all cases. Specifically, we first investigate why IW may fail in cases (iii) and (iv); based on the findings, we propose generalized IW (GIW) that could handle cases (iii) and (iv) and would reduce to IW in cases (i) and (ii). In GIW, the test support is split into an in-training (IT) part and an out-of-training (OOT) part, and the expected risk is decomposed into a weighted classification term over the IT part and a standard classification term over the OOT part, which guarantees the risk consistency of GIW. Then, the implementation of GIW consists of three components: (a) the split of validation data is carried out by the one-class support vector machine, (b) the first term of the empirical risk can be handled by any IW algorithm given training data and IT validation data, and (c) the second term just involves OOT validation data. Experiments demonstrate that GIW is a universal solver for DS problems, outperforming IW methods in cases (iii) and (iv).

Rethinking Importance Weighting for Transfer Learning

A key assumption in supervised learning is that training and test data follow the same probability distribution. However, this fundamental assumption is not always satisfied in practice, e.g., due to changing environments, sample selection bias, privacy concerns, or high labeling costs. Transfer learning (TL) relaxes this assumption and allows us to learn under distribution shift. Classical TL methods typically rely on importance-weighting -- a predictor is trained based on the training losses weighted according to the importance (i.e., the test-over-training density ratio). However, as real-world machine learning tasks are becoming increasingly complex, high-dimensional, and dynamical, novel approaches are explored to cope with such challenges recently. In this article, after introducing the foundation of TL based on importance-weighting, we review recent advances based on joint and dynamic importance-predictor estimation. Furthermore, we introduce a method of causal mechanism transfer that incorporates causal structure in TL. Finally, we discuss future perspectives of TL research.

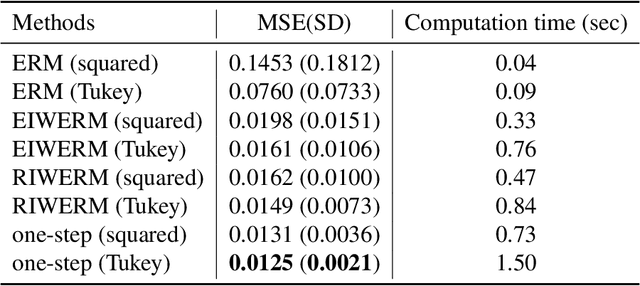
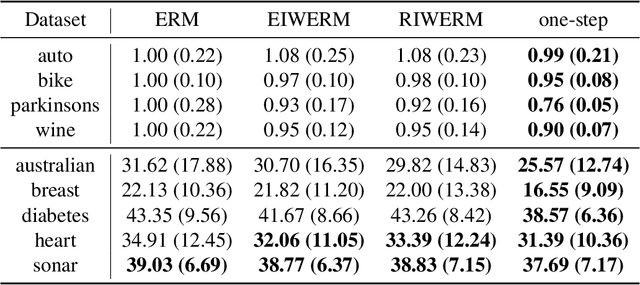
Rethinking Importance Weighting for Deep Learning under Distribution Shift

Under distribution shift (DS) where the training data distribution differs from the test one, a powerful technique is importance weighting (IW) which handles DS in two separate steps: weight estimation (WE) estimates the test-over-training density ratio and weighted classification (WC) trains the classifier from weighted training data. However, IW cannot work well on complex data, since WE is incompatible with deep learning. In this paper, we rethink IW and theoretically show it suffers from a circular dependency: we need not only WE for WC, but also WC for WE where a trained deep classifier is used as the feature extractor (FE). To cut off the dependency, we try to pretrain FE from unweighted training data, which leads to biased FE. To overcome the bias, we propose an end-to-end solution dynamic IW that iterates between WE and WC and combines them in a seamless manner, and hence our WE can also enjoy deep networks and stochastic optimizers indirectly. Experiments with two representative DSs on Fashion-MNIST and CIFAR-10/100 demonstrate that dynamic IW compares favorably with state-of-the-art methods.