Understanding Generalization in Physics Informed Models through Affine Variety Dimensions

In recent years, physics-informed machine learning has gained significant attention for its ability to enhance statistical performance and sample efficiency by integrating physical structures into machine learning models. These structures, such as differential equations, conservation laws, and symmetries, serve as inductive biases that can improve the generalization capacity of the hybrid model. However, the mechanisms by which these physical structures enhance generalization capacity are not fully understood, limiting the ability to guarantee the performance of the models. In this study, we show that the generalization performance of linear regressors incorporating differential equation structures is determined by the dimension of the associated affine variety, rather than the number of parameters. This finding enables a unified analysis of various equations, including nonlinear ones. We introduce a method to approximate the dimension of the affine variety and provide experimental evidence to validate our theoretical insights.

Initialization Bias of Fourier Neural Operator: Revisiting the Edge of Chaos

This paper investigates the initialization bias of the Fourier neural operator (FNO). A mean-field theory for FNO is established, analyzing the behavior of the random FNO from an ``edge of chaos'' perspective. We uncover that the forward and backward propagation behaviors exhibit characteristics unique to FNO, induced by mode truncation, while also showcasing similarities to those of densely connected networks. Building upon this observation, we also propose a FNO version of the He initialization scheme to mitigate the negative initialization bias leading to training instability. Experimental results demonstrate the effectiveness of our initialization scheme, enabling stable training of a 32-layer FNO without the need for additional techniques or significant performance degradation.

Neural Lagrangian Schrödinger Bridge

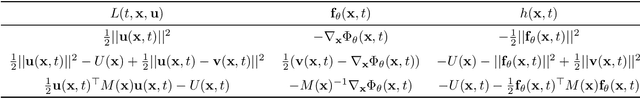
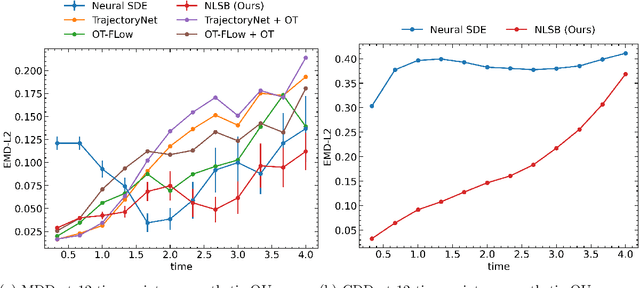
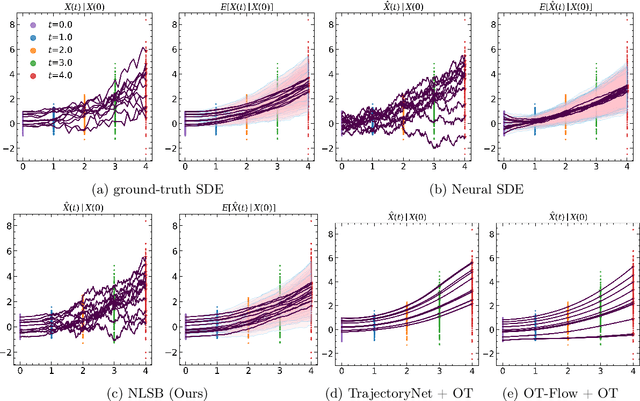
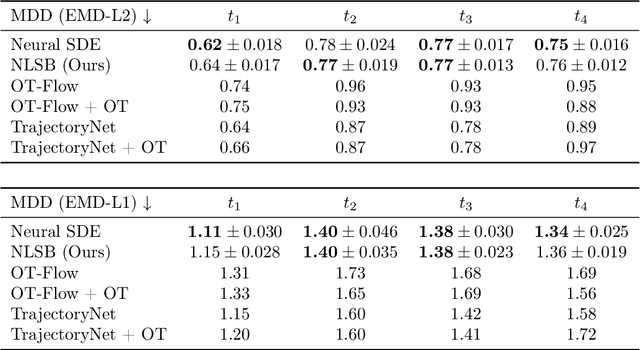
Population dynamics is the study of temporal and spatial variation in the size of populations of organisms and is a major part of population ecology. One of the main difficulties in analyzing population dynamics is that we can only obtain observation data with coarse time intervals from fixed-point observations due to experimental costs or other constraints. Recently, modeling population dynamics by using continuous normalizing flows (CNFs) and dynamic optimal transport has been proposed to infer the expected trajectory of samples from a fixed-point observed population. While the sample behavior in CNF is deterministic, the actual sample in biological systems moves in an essentially random yet directional manner. Moreover, when a sample moves from point A to point B in dynamical systems, its trajectory is such that the corresponding action has the smallest possible value, known as the principle of least action. To satisfy these requirements of the sample trajectories, we formulate the Lagrangian Schr\"odinger bridge (LSB) problem and propose to solve it approximately using neural SDE with regularization. We also develop a model architecture that enables faster computation. Our experiments show that our solution to the LSB problem can approximate the dynamics at the population level and that using the prior knowledge introduced by the Lagrangian enables us to estimate the trajectories of individual samples with stochastic behavior.