Blitzkriging: Kronecker-structured Stochastic Gaussian Processes

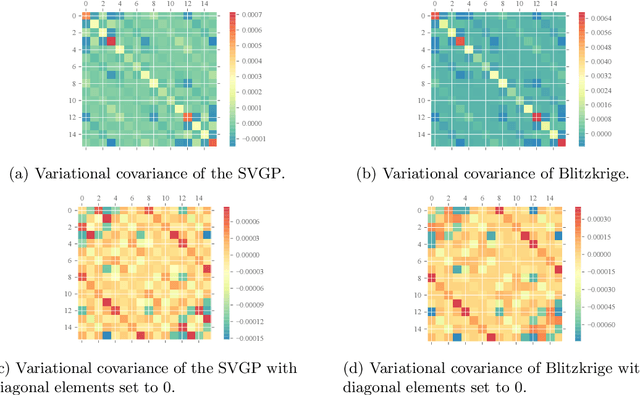
We present Blitzkriging, a new approach to fast inference for Gaussian processes, applicable to regression, optimisation and classification. State-of-the-art (stochastic) inference for Gaussian processes on very large datasets scales cubically in the number of 'inducing inputs', variables introduced to factorise the model. Blitzkriging shares state-of-the-art scaling with data, but reduces the scaling in the number of inducing points to approximately linear. Further, in contrast to other methods, Blitzkriging: does not force the data to conform to any particular structure (including grid-like); reduces reliance on error-prone optimisation of inducing point locations; and is able to learn rich (covariance) structure from the data. We demonstrate the benefits of our approach on real data in regression, time-series prediction and signal-interpolation experiments.

Variational Inference for Gaussian Process Modulated Poisson Processes

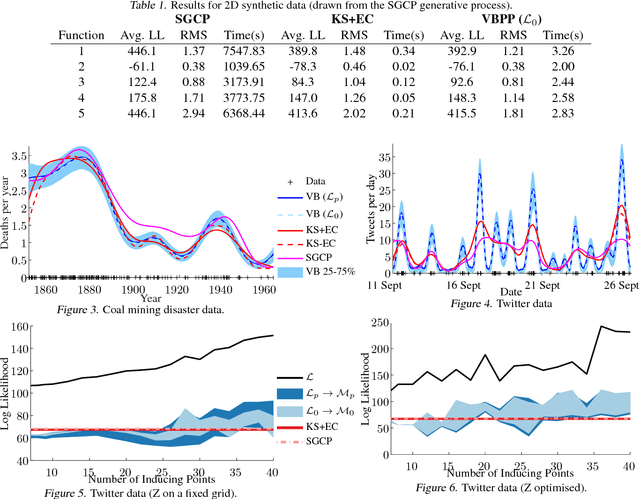
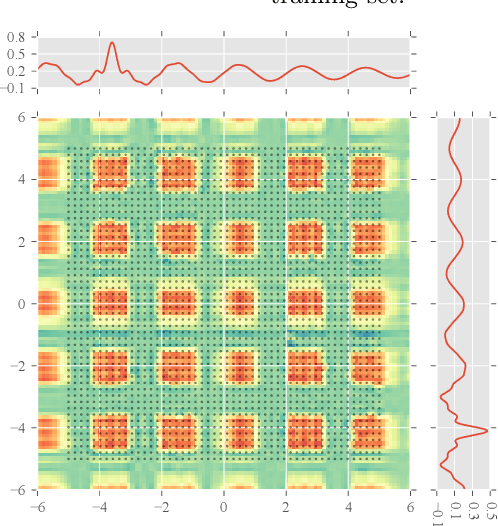
We present the first fully variational Bayesian inference scheme for continuous Gaussian-process-modulated Poisson processes. Such point processes are used in a variety of domains, including neuroscience, geo-statistics and astronomy, but their use is hindered by the computational cost of existing inference schemes. Our scheme: requires no discretisation of the domain; scales linearly in the number of observed events; and is many orders of magnitude faster than previous sampling based approaches. The resulting algorithm is shown to outperform standard methods on synthetic examples, coal mining disaster data and in the prediction of Malaria incidences in Kenya.

Efficient Bayesian Nonparametric Modelling of Structured Point Processes

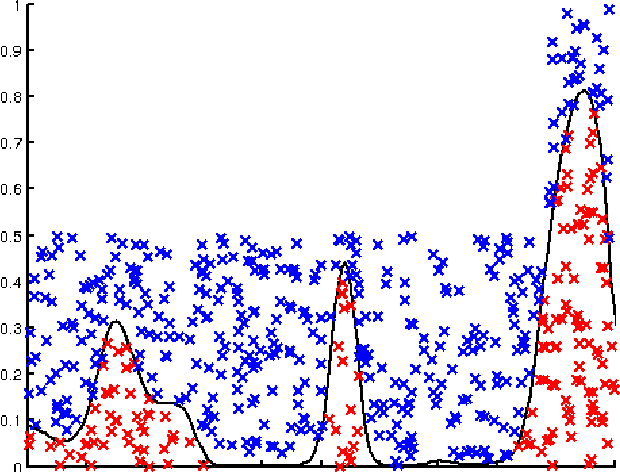
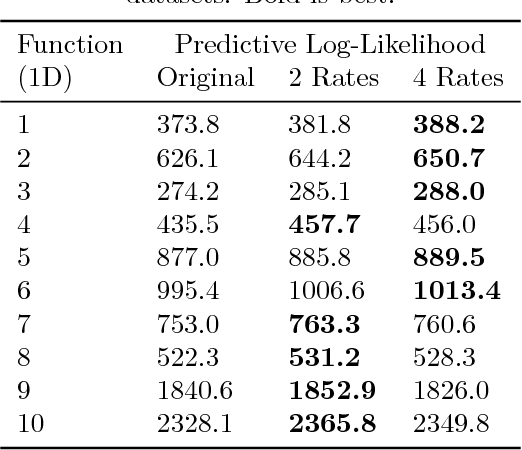
This paper presents a Bayesian generative model for dependent Cox point processes, alongside an efficient inference scheme which scales as if the point processes were modelled independently. We can handle missing data naturally, infer latent structure, and cope with large numbers of observed processes. A further novel contribution enables the model to work effectively in higher dimensional spaces. Using this method, we achieve vastly improved predictive performance on both 2D and 1D real data, validating our structured approach.