Variational Inference for Gaussian Process Modulated Poisson Processes
Paper and Code
Jul 27, 2015
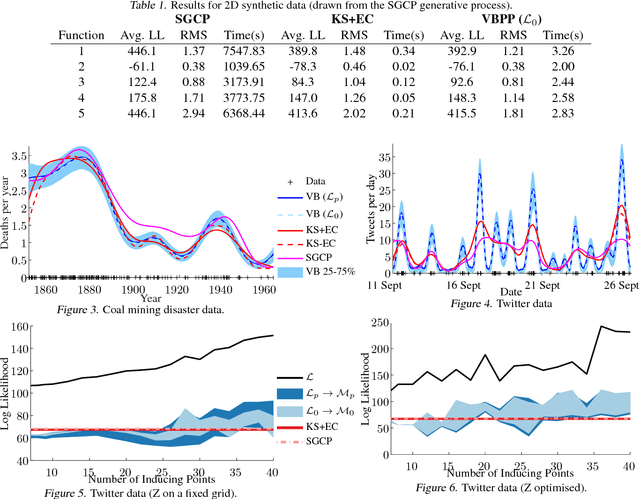


We present the first fully variational Bayesian inference scheme for continuous Gaussian-process-modulated Poisson processes. Such point processes are used in a variety of domains, including neuroscience, geo-statistics and astronomy, but their use is hindered by the computational cost of existing inference schemes. Our scheme: requires no discretisation of the domain; scales linearly in the number of observed events; and is many orders of magnitude faster than previous sampling based approaches. The resulting algorithm is shown to outperform standard methods on synthetic examples, coal mining disaster data and in the prediction of Malaria incidences in Kenya.
* in ICML 2015
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge