CuDA2: An approach for Incorporating Traitor Agents into Cooperative Multi-Agent Systems

Cooperative Multi-Agent Reinforcement Learning (CMARL) strategies are well known to be vulnerable to adversarial perturbations. Previous works on adversarial attacks have primarily focused on white-box attacks that directly perturb the states or actions of victim agents, often in scenarios with a limited number of attacks. However, gaining complete access to victim agents in real-world environments is exceedingly difficult. To create more realistic adversarial attacks, we introduce a novel method that involves injecting traitor agents into the CMARL system. We model this problem as a Traitor Markov Decision Process (TMDP), where traitors cannot directly attack the victim agents but can influence their formation or positioning through collisions. In TMDP, traitors are trained using the same MARL algorithm as the victim agents, with their reward function set as the negative of the victim agents' reward. Despite this, the training efficiency for traitors remains low because it is challenging for them to directly associate their actions with the victim agents' rewards. To address this issue, we propose the Curiosity-Driven Adversarial Attack (CuDA2) framework. CuDA2 enhances the efficiency and aggressiveness of attacks on the specified victim agents' policies while maintaining the optimal policy invariance of the traitors. Specifically, we employ a pre-trained Random Network Distillation (RND) module, where the extra reward generated by the RND module encourages traitors to explore states unencountered by the victim agents. Extensive experiments on various scenarios from SMAC demonstrate that our CuDA2 framework offers comparable or superior adversarial attack capabilities compared to other baselines.

HiBid: A Cross-Channel Constrained Bidding System with Budget Allocation by Hierarchical Offline Deep Reinforcement Learning

Online display advertising platforms service numerous advertisers by providing real-time bidding (RTB) for the scale of billions of ad requests every day. The bidding strategy handles ad requests cross multiple channels to maximize the number of clicks under the set financial constraints, i.e., total budget and cost-per-click (CPC), etc. Different from existing works mainly focusing on single channel bidding, we explicitly consider cross-channel constrained bidding with budget allocation. Specifically, we propose a hierarchical offline deep reinforcement learning (DRL) framework called ``HiBid'', consisted of a high-level planner equipped with auxiliary loss for non-competitive budget allocation, and a data augmentation enhanced low-level executor for adaptive bidding strategy in response to allocated budgets. Additionally, a CPC-guided action selection mechanism is introduced to satisfy the cross-channel CPC constraint. Through extensive experiments on both the large-scale log data and online A/B testing, we confirm that HiBid outperforms six baselines in terms of the number of clicks, CPC satisfactory ratio, and return-on-investment (ROI). We also deploy HiBid on Meituan advertising platform to already service tens of thousands of advertisers every day.

Semi-Centralised Multi-Agent Reinforcement Learning with Policy-Embedded Training

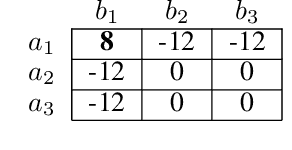
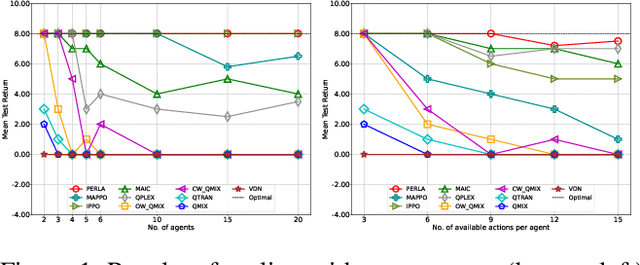
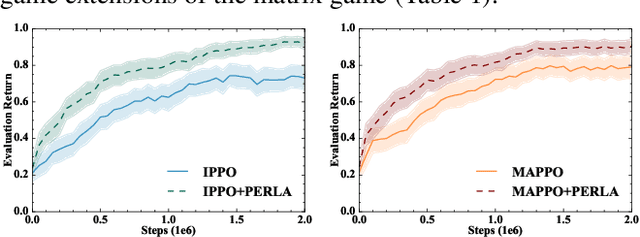
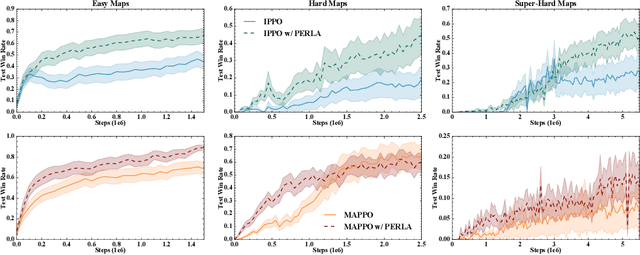
Centralised training (CT) is the basis for many popular multi-agent reinforcement learning (MARL) methods because it allows agents to quickly learn high-performing policies. However, CT relies on agents learning from one-off observations of other agents' actions at a given state. Because MARL agents explore and update their policies during training, these observations often provide poor predictions about other agents' behaviour and the expected return for a given action. CT methods therefore suffer from high variance and error-prone estimates, harming learning. CT methods also suffer from explosive growth in complexity due to the reliance on global observations, unless strong factorisation restrictions are imposed (e.g., monotonic reward functions for QMIX). We address these challenges with a new semi-centralised MARL framework that performs policy-embedded training and decentralised execution. Our method, policy embedded reinforcement learning algorithm (PERLA), is an enhancement tool for Actor-Critic MARL algorithms that leverages a novel parameter sharing protocol and policy embedding method to maintain estimates that account for other agents' behaviour. Our theory proves PERLA dramatically reduces the variance in value estimates. Unlike various CT methods, PERLA, which seamlessly adopts MARL algorithms, scales easily with the number of agents without the need for restrictive factorisation assumptions. We demonstrate PERLA's superior empirical performance and efficient scaling in benchmark environments including StarCraft Micromanagement II and Multi-agent Mujoco

Timing is Everything: Learning to Act Selectively with Costly Actions and Budgetary Constraints

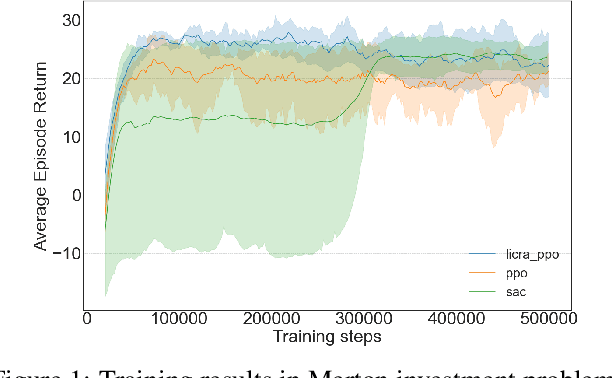
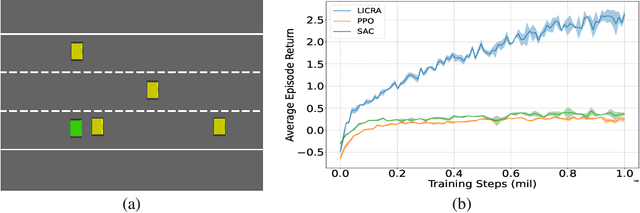
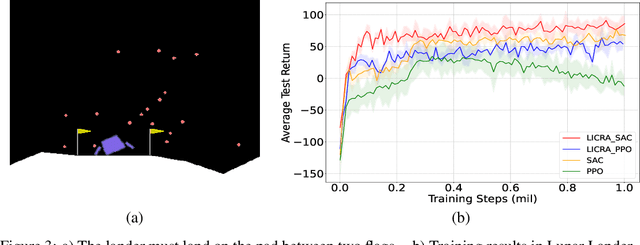
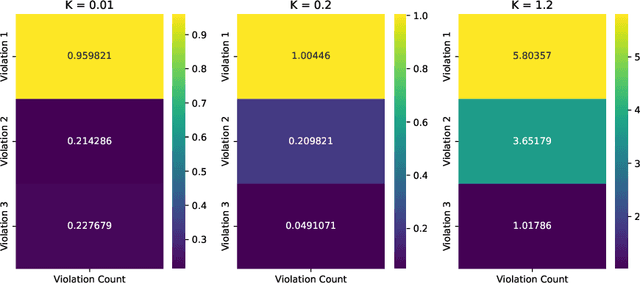
Many real-world settings involve costs for performing actions; transaction costs in financial systems and fuel costs being common examples. In these settings, performing actions at each time step quickly accumulates costs leading to vastly suboptimal outcomes. Additionally, repeatedly acting produces wear and tear and ultimately, damage. Determining when to act is crucial for achieving successful outcomes and yet, the challenge of efficiently learning to behave optimally when actions incur minimally bounded costs remains unresolved. In this paper, we introduce a reinforcement learning (RL) framework named Learnable Impulse Control Reinforcement Algorithm (LICRA), for learning to optimally select both when to act and which actions to take when actions incur costs. At the core of LICRA is a nested structure that combines RL and a form of policy known as impulse control which learns to maximise objectives when actions incur costs. We prove that LICRA, which seamlessly adopts any RL method, converges to policies that optimally select when to perform actions and their optimal magnitudes. We then augment LICRA to handle problems in which the agent can perform at most $k<\infty$ actions and more generally, faces a budget constraint. We show LICRA learns the optimal value function and ensures budget constraints are satisfied almost surely. We demonstrate empirically LICRA's superior performance against benchmark RL methods in OpenAI gym's Lunar Lander and in Highway environments and a variant of the Merton portfolio problem within finance.