Approximate Nash Equilibrium Learning for n-Player Markov Games in Dynamic Pricing
Paper and Code
Jul 13, 2022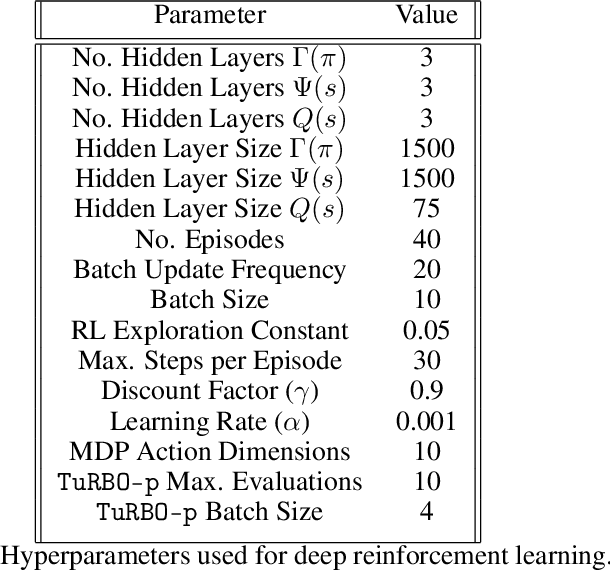
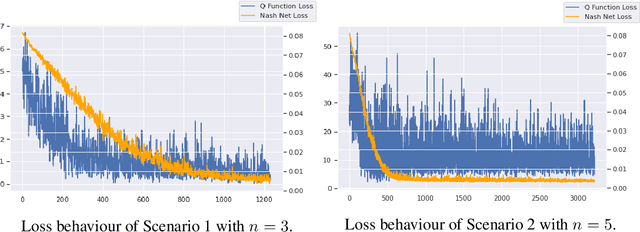
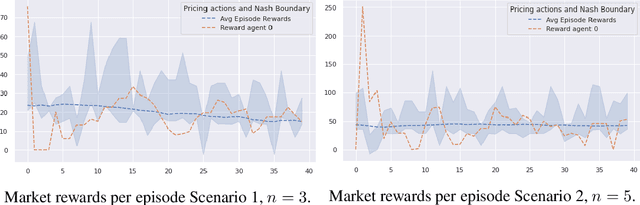
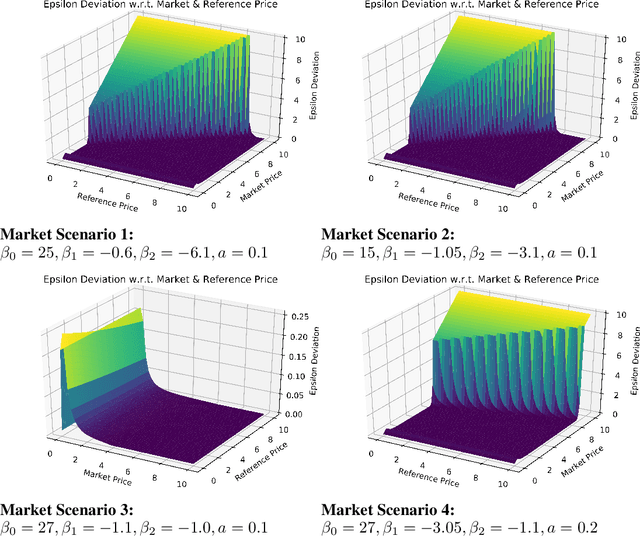
We investigate Nash equilibrium learning in a competitive Markov Game (MG) environment, where multiple agents compete, and multiple Nash equilibria can exist. In particular, for an oligopolistic dynamic pricing environment, exact Nash equilibria are difficult to obtain due to the curse-of-dimensionality. We develop a new model-free method to find approximate Nash equilibria. Gradient-free black box optimization is then applied to estimate $\epsilon$, the maximum reward advantage of an agent unilaterally deviating from any joint policy, and to also estimate the $\epsilon$-minimizing policy for any given state. The policy-$\epsilon$ correspondence and the state to $\epsilon$-minimizing policy are represented by neural networks, the latter being the Nash Policy Net. During batch update, we perform Nash Q learning on the system, by adjusting the action probabilities using the Nash Policy Net. We demonstrate that an approximate Nash equilibrium can be learned, particularly in the dynamic pricing domain where exact solutions are often intractable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge