Causal Bandits without Graph Learning

We study the causal bandit problem when the causal graph is unknown and develop an efficient algorithm for finding the parent node of the reward node using atomic interventions. We derive the exact equation for the expected number of interventions performed by the algorithm and show that under certain graphical conditions it could perform either logarithmically fast or, under more general assumptions, slower but still sublinearly in the number of variables. We formally show that our algorithm is optimal as it meets the universal lower bound we establish for any algorithm that performs atomic interventions. Finally, we extend our algorithm to the case when the reward node has multiple parents. Using this algorithm together with a standard algorithm from bandit literature leads to improved regret bounds.

Trace norm regularization for multi-task learning with scarce data

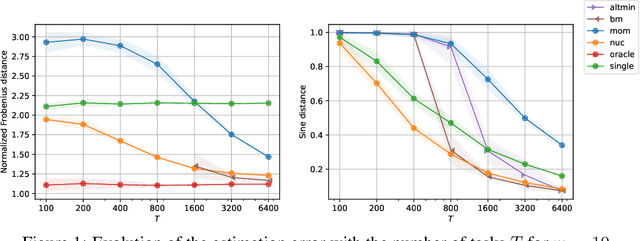
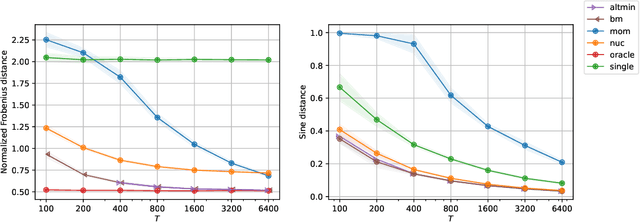
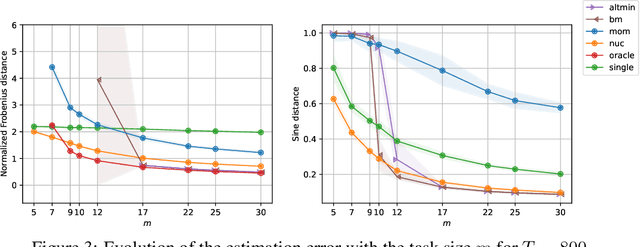
Multi-task learning leverages structural similarities between multiple tasks to learn despite very few samples. Motivated by the recent success of neural networks applied to data-scarce tasks, we consider a linear low-dimensional shared representation model. Despite an extensive literature, existing theoretical results either guarantee weak estimation rates or require a large number of samples per task. This work provides the first estimation error bound for the trace norm regularized estimator when the number of samples per task is small. The advantages of trace norm regularization for learning data-scarce tasks extend to meta-learning and are confirmed empirically on synthetic datasets.

Meta-Thompson Sampling

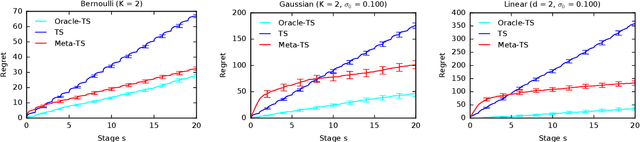
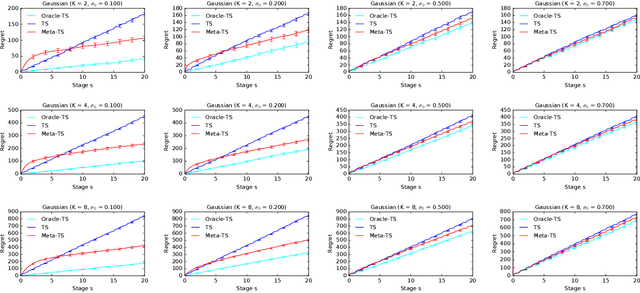
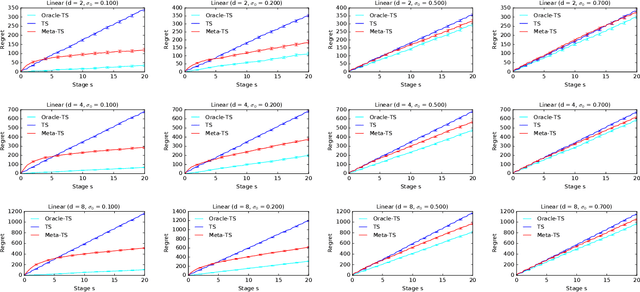
Efficient exploration in multi-armed bandits is a fundamental online learning problem. In this work, we propose a variant of Thompson sampling that learns to explore better as it interacts with problem instances drawn from an unknown prior distribution. Our algorithm meta-learns the prior and thus we call it Meta-TS. We propose efficient implementations of Meta-TS and analyze it in Gaussian bandits. Our analysis shows the benefit of meta-learning the prior and is of a broader interest, because we derive the first prior-dependent upper bound on the Bayes regret of Thompson sampling. This result is complemented by empirical evaluation, which shows that Meta-TS quickly adapts to the unknown prior.

On Optimality of Meta-Learning in Fixed-Design Regression with Weighted Biased Regularization

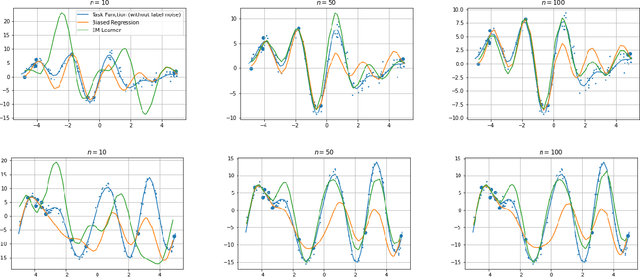
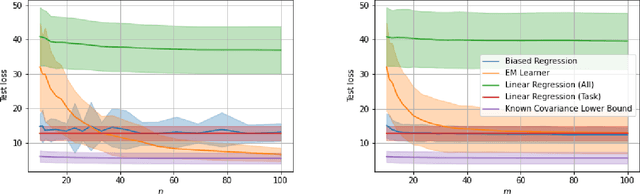
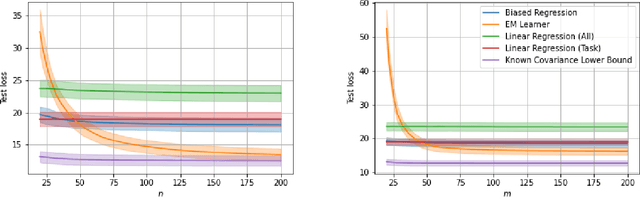
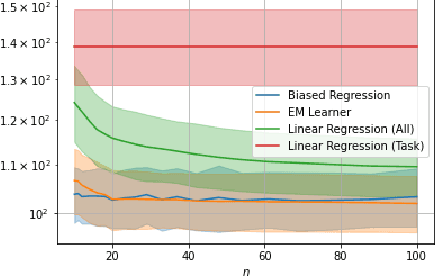
We consider a fixed-design linear regression in the meta-learning model of Baxter (2000) and establish a problem-dependent finite-sample lower bound on the transfer risk (risk on a newly observed task) valid for all estimators. Moreover, we prove that a weighted form of a biased regularization - a popular technique in transfer and meta-learning - is optimal, i.e. it enjoys a problem-dependent upper bound on the risk matching our lower bound up to a constant. Thus, our bounds characterize meta-learning linear regression problems and reveal a fine-grained dependency on the task structure. Our characterization suggests that in the non-asymptotic regime, for a sufficiently large number of tasks, meta-learning can be considerably superior to a single-task learning. Finally, we propose a practical adaptation of the optimal estimator through Expectation-Maximization procedure and show its effectiveness in series of experiments.