On Optimality of Meta-Learning in Fixed-Design Regression with Weighted Biased Regularization

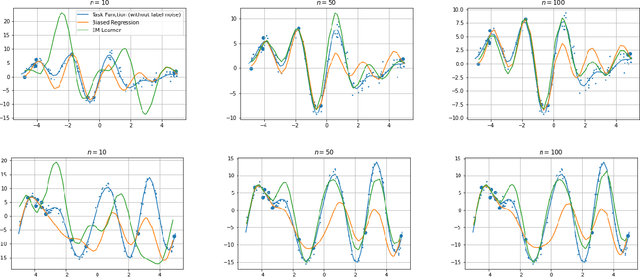
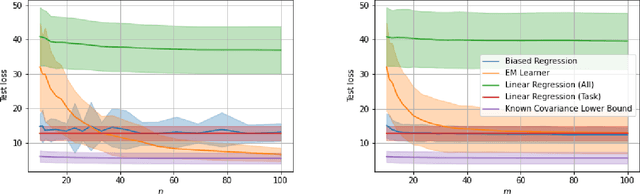
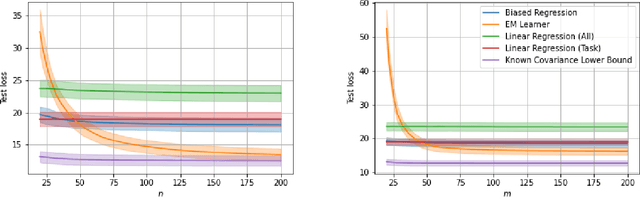
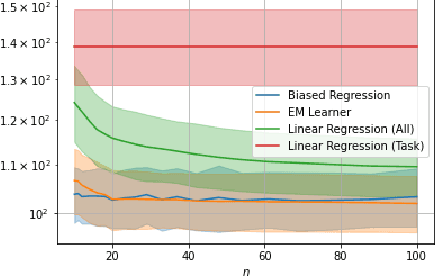
We consider a fixed-design linear regression in the meta-learning model of Baxter (2000) and establish a problem-dependent finite-sample lower bound on the transfer risk (risk on a newly observed task) valid for all estimators. Moreover, we prove that a weighted form of a biased regularization - a popular technique in transfer and meta-learning - is optimal, i.e. it enjoys a problem-dependent upper bound on the risk matching our lower bound up to a constant. Thus, our bounds characterize meta-learning linear regression problems and reveal a fine-grained dependency on the task structure. Our characterization suggests that in the non-asymptotic regime, for a sufficiently large number of tasks, meta-learning can be considerably superior to a single-task learning. Finally, we propose a practical adaptation of the optimal estimator through Expectation-Maximization procedure and show its effectiveness in series of experiments.