Meta-Thompson Sampling
Paper and Code
Feb 11, 2021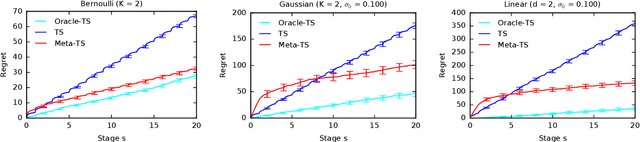
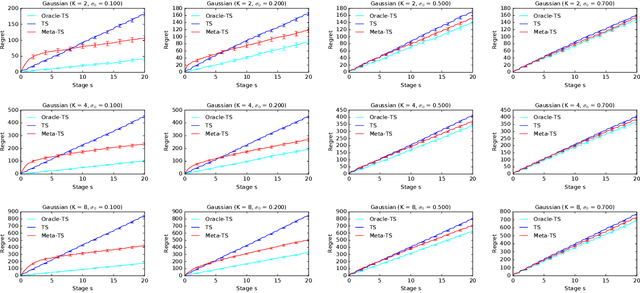
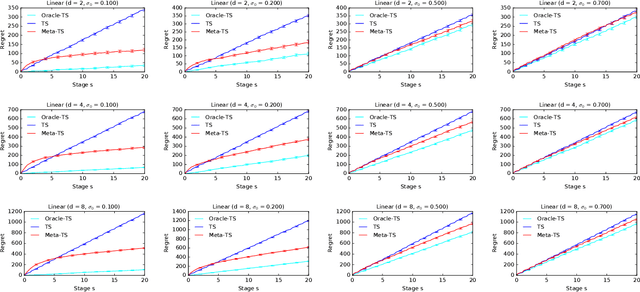
Efficient exploration in multi-armed bandits is a fundamental online learning problem. In this work, we propose a variant of Thompson sampling that learns to explore better as it interacts with problem instances drawn from an unknown prior distribution. Our algorithm meta-learns the prior and thus we call it Meta-TS. We propose efficient implementations of Meta-TS and analyze it in Gaussian bandits. Our analysis shows the benefit of meta-learning the prior and is of a broader interest, because we derive the first prior-dependent upper bound on the Bayes regret of Thompson sampling. This result is complemented by empirical evaluation, which shows that Meta-TS quickly adapts to the unknown prior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge