Enhancing Privacy against Inversion Attacks in Federated Learning by using Mixing Gradients Strategies

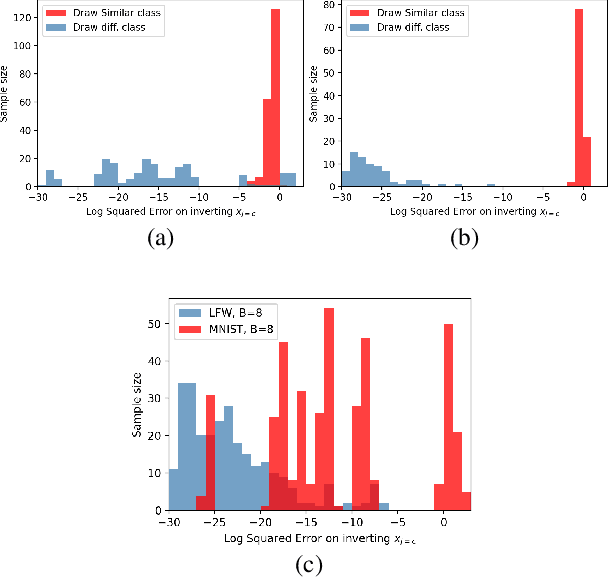
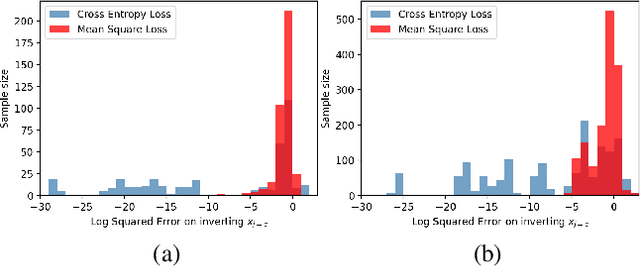
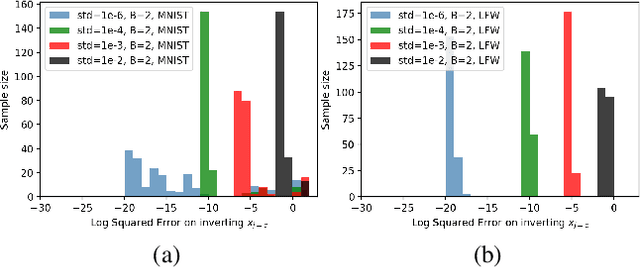
Federated learning reduces the risk of information leakage, but remains vulnerable to attacks. We investigate how several neural network design decisions can defend against gradients inversion attacks. We show that overlapping gradients provides numerical resistance to gradient inversion on the highly vulnerable dense layer. Specifically, we propose to leverage batching to maximise mixing of gradients by choosing an appropriate loss function and drawing identical labels. We show that otherwise it is possible to directly recover all vectors in a mini-batch without any numerical optimisation due to the de-mixing nature of the cross entropy loss. To accurately assess data recovery, we introduce an absolute variation distance (AVD) metric for information leakage in images, derived from total variation. In contrast to standard metrics, e.g. Mean Squared Error or Structural Similarity Index, AVD offers a continuous metric for extracting information in noisy images. Finally, our empirical results on information recovery from various inversion attacks and training performance supports our defense strategies. These strategies are also shown to be useful for deep convolutional neural networks such as LeNET for image recognition. We hope that this study will help guide the development of further strategies that achieve a trustful federation policy.

Copula Flows for Synthetic Data Generation

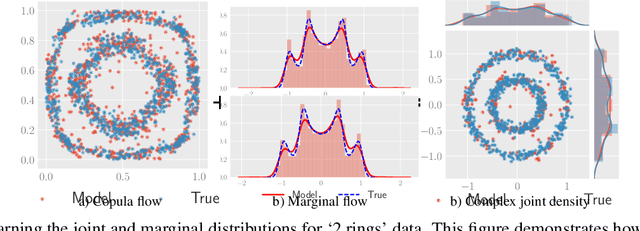
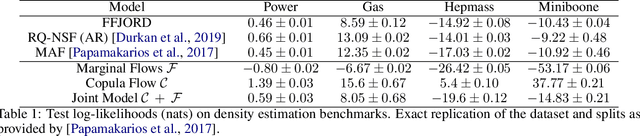
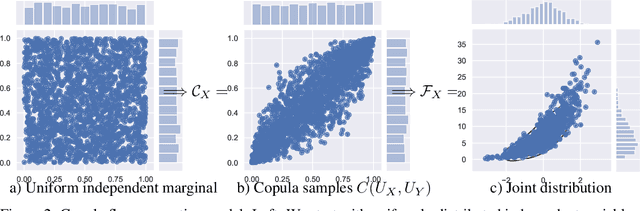
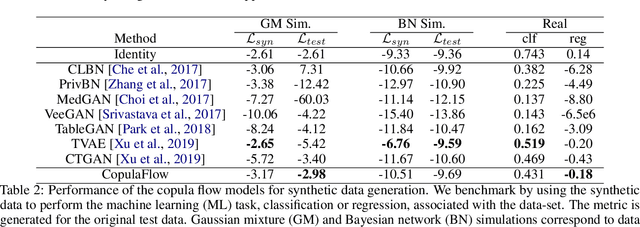
The ability to generate high-fidelity synthetic data is crucial when available (real) data is limited or where privacy and data protection standards allow only for limited use of the given data, e.g., in medical and financial data-sets. Current state-of-the-art methods for synthetic data generation are based on generative models, such as Generative Adversarial Networks (GANs). Even though GANs have achieved remarkable results in synthetic data generation, they are often challenging to interpret.Furthermore, GAN-based methods can suffer when used with mixed real and categorical variables.Moreover, loss function (discriminator loss) design itself is problem specific, i.e., the generative model may not be useful for tasks it was not explicitly trained for. In this paper, we propose to use a probabilistic model as a synthetic data generator. Learning the probabilistic model for the data is equivalent to estimating the density of the data. Based on the copula theory, we divide the density estimation task into two parts, i.e., estimating univariate marginals and estimating the multivariate copula density over the univariate marginals. We use normalising flows to learn both the copula density and univariate marginals. We benchmark our method on both simulated and real data-sets in terms of density estimation as well as the ability to generate high-fidelity synthetic data

Data-Efficient Reinforcement Learning with Probabilistic Model Predictive Control

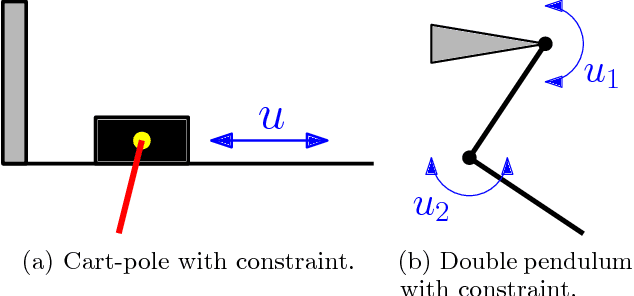
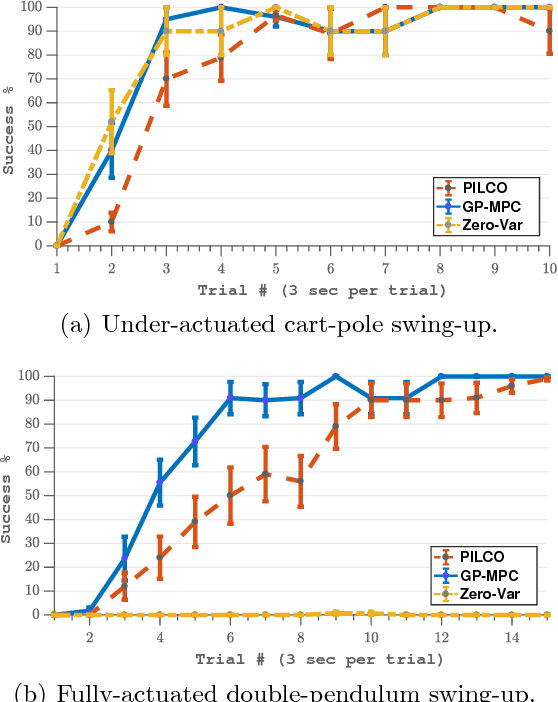
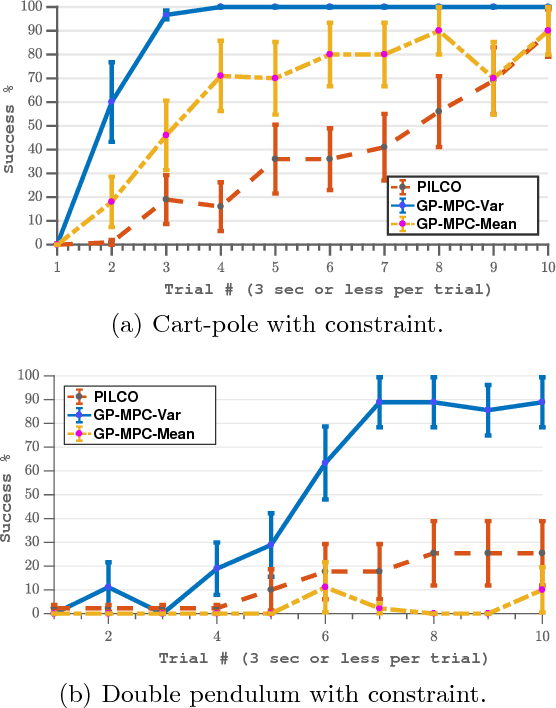
Trial-and-error based reinforcement learning (RL) has seen rapid advancements in recent times, especially with the advent of deep neural networks. However, the majority of autonomous RL algorithms require a large number of interactions with the environment. A large number of interactions may be impractical in many real-world applications, such as robotics, and many practical systems have to obey limitations in the form of state space or control constraints. To reduce the number of system interactions while simultaneously handling constraints, we propose a model-based RL framework based on probabilistic Model Predictive Control (MPC). In particular, we propose to learn a probabilistic transition model using Gaussian Processes (GPs) to incorporate model uncertainty into long-term predictions, thereby, reducing the impact of model errors. We then use MPC to find a control sequence that minimises the expected long-term cost. We provide theoretical guarantees for first-order optimality in the GP-based transition models with deterministic approximate inference for long-term planning. We demonstrate that our approach does not only achieve state-of-the-art data efficiency, but also is a principled way for RL in constrained environments.