Chuwei Wang
EquiReg: Equivariance Regularized Diffusion for Inverse Problems
May 29, 2025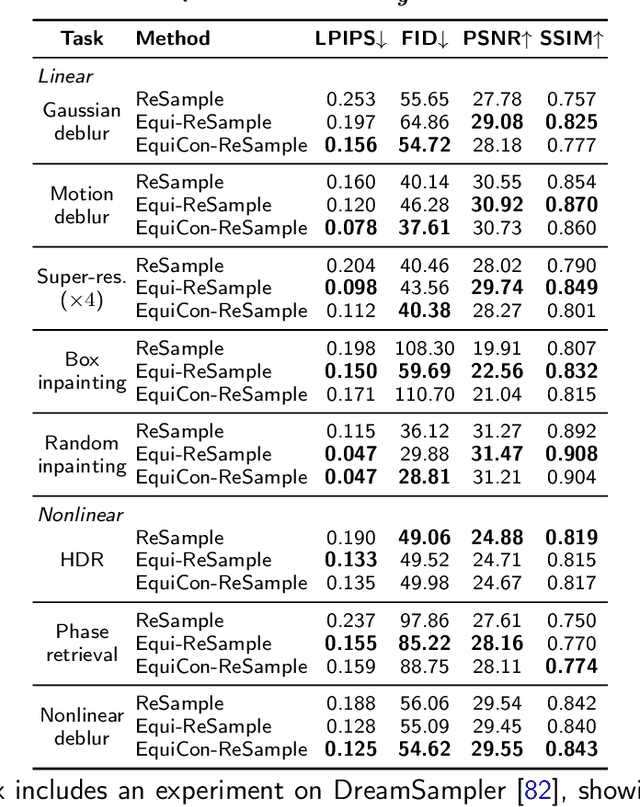
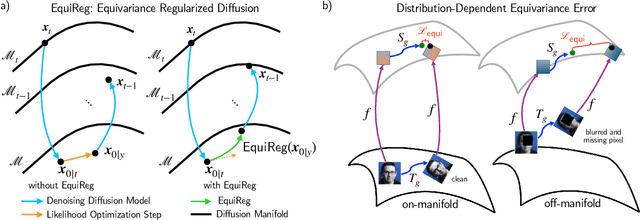
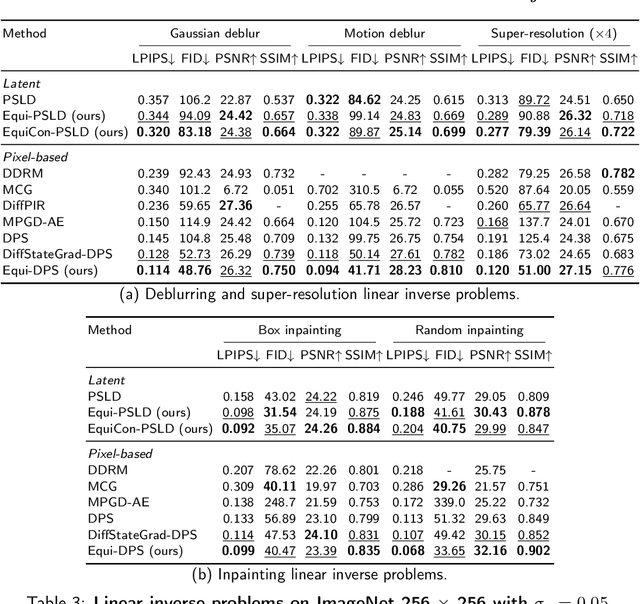
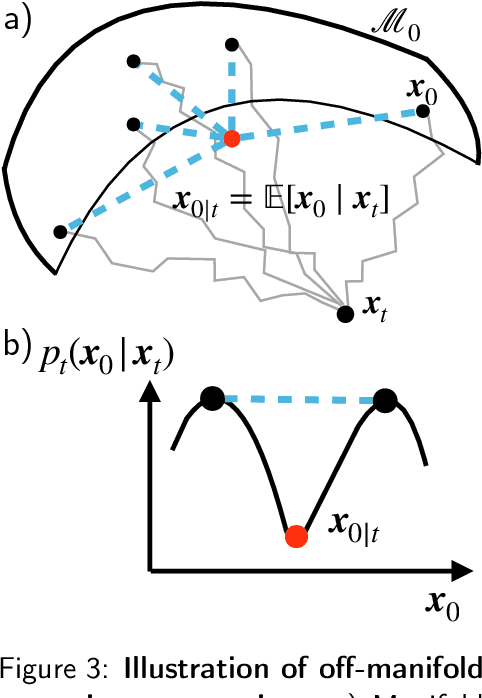
Abstract:Diffusion models represent the state-of-the-art for solving inverse problems such as image restoration tasks. In the Bayesian framework, diffusion-based inverse solvers incorporate a likelihood term to guide the prior sampling process, generating data consistent with the posterior distribution. However, due to the intractability of the likelihood term, many current methods rely on isotropic Gaussian approximations, which lead to deviations from the data manifold and result in inconsistent, unstable reconstructions. We propose Equivariance Regularized (EquiReg) diffusion, a general framework for regularizing posterior sampling in diffusion-based inverse problem solvers. EquiReg enhances reconstructions by reweighting diffusion trajectories and penalizing those that deviate from the data manifold. We define a new distribution-dependent equivariance error, empirically identify functions that exhibit low error for on-manifold samples and higher error for off-manifold samples, and leverage these functions to regularize the diffusion sampling process. When applied to a variety of solvers, EquiReg outperforms state-of-the-art diffusion models in both linear and nonlinear image restoration tasks, as well as in reconstructing partial differential equations.
Beyond Closure Models: Learning Chaotic-Systems via Physics-Informed Neural Operators
Aug 09, 2024Abstract:Accurately predicting the long-term behavior of chaotic systems is crucial for various applications such as climate modeling. However, achieving such predictions typically requires iterative computations over a dense spatiotemporal grid to account for the unstable nature of chaotic systems, which is expensive and impractical in many real-world situations. An alternative approach to such a full-resolved simulation is using a coarse grid and then correcting its errors through a \textit{closure model}, which approximates the overall information from fine scales not captured in the coarse-grid simulation. Recently, ML approaches have been used for closure modeling, but they typically require a large number of training samples from expensive fully-resolved simulations (FRS). In this work, we prove an even more fundamental limitation, i.e., the standard approach to learning closure models suffers from a large approximation error for generic problems, no matter how large the model is, and it stems from the non-uniqueness of the mapping. We propose an alternative end-to-end learning approach using a physics-informed neural operator (PINO) that overcomes this limitation by not using a closure model or a coarse-grid solver. We first train the PINO model on data from a coarse-grid solver and then fine-tune it with (a small amount of) FRS and physics-based losses on a fine grid. The discretization-free nature of neural operators means that they do not suffer from the restriction of a coarse grid that closure models face, and they can provably approximate the long-term statistics of chaotic systems. In our experiments, our PINO model achieves a 120x speedup compared to FRS with a relative error $\sim 5\%$. In contrast, the closure model coupled with a coarse-grid solver is $58$x slower than PINO while having a much higher error $\sim205\%$ when the closure model is trained on the same FRS dataset.
DOF: Accelerating High-order Differential Operators with Forward Propagation
Feb 15, 2024



Abstract:Solving partial differential equations (PDEs) efficiently is essential for analyzing complex physical systems. Recent advancements in leveraging deep learning for solving PDE have shown significant promise. However, machine learning methods, such as Physics-Informed Neural Networks (PINN), face challenges in handling high-order derivatives of neural network-parameterized functions. Inspired by Forward Laplacian, a recent method of accelerating Laplacian computation, we propose an efficient computational framework, Differential Operator with Forward-propagation (DOF), for calculating general second-order differential operators without losing any precision. We provide rigorous proof of the advantages of our method over existing methods, demonstrating two times improvement in efficiency and reduced memory consumption on any architectures. Empirical results illustrate that our method surpasses traditional automatic differentiation (AutoDiff) techniques, achieving 2x improvement on the MLP structure and nearly 20x improvement on the MLP with Jacobian sparsity.
Forward Laplacian: A New Computational Framework for Neural Network-based Variational Monte Carlo
Jul 17, 2023Abstract:Neural network-based variational Monte Carlo (NN-VMC) has emerged as a promising cutting-edge technique of ab initio quantum chemistry. However, the high computational cost of existing approaches hinders their applications in realistic chemistry problems. Here, we report the development of a new NN-VMC method that achieves a remarkable speed-up by more than one order of magnitude, thereby greatly extending the applicability of NN-VMC to larger systems. Our key design is a novel computational framework named Forward Laplacian, which computes the Laplacian associated with neural networks, the bottleneck of NN-VMC, through an efficient forward propagation process. We then demonstrate that Forward Laplacian is not only versatile but also facilitates more developments of acceleration methods across various aspects, including optimization for sparse derivative matrix and efficient neural network design. Empirically, our approach enables NN-VMC to investigate a broader range of atoms, molecules and chemical reactions for the first time, providing valuable references to other ab initio methods. The results demonstrate a great potential in applying deep learning methods to solve general quantum mechanical problems.
Is $L^2$ Physics-Informed Loss Always Suitable for Training Physics-Informed Neural Network?
Jun 04, 2022
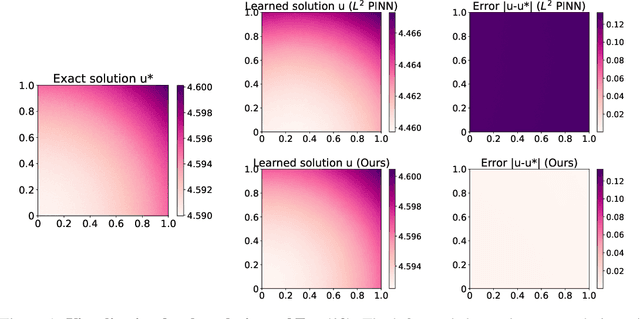
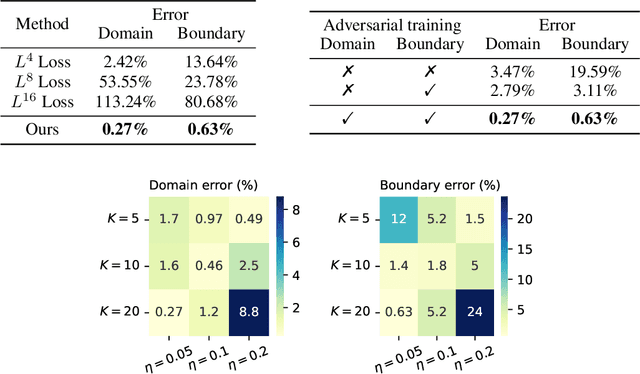
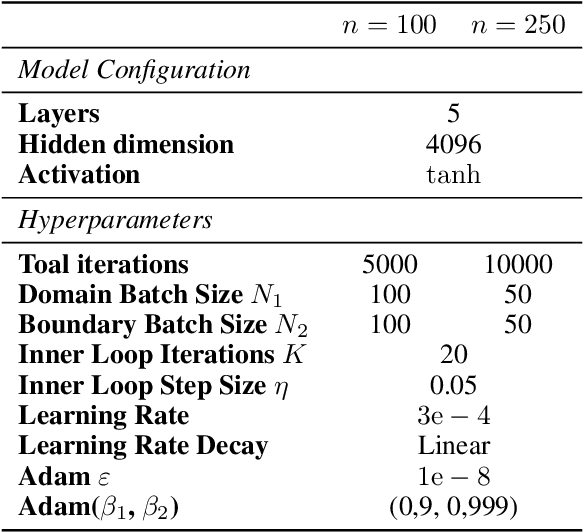
Abstract:The Physics-Informed Neural Network (PINN) approach is a new and promising way to solve partial differential equations using deep learning. The $L^2$ Physics-Informed Loss is the de-facto standard in training Physics-Informed Neural Networks. In this paper, we challenge this common practice by investigating the relationship between the loss function and the approximation quality of the learned solution. In particular, we leverage the concept of stability in the literature of partial differential equation to study the asymptotic behavior of the learned solution as the loss approaches zero. With this concept, we study an important class of high-dimensional non-linear PDEs in optimal control, the Hamilton-Jacobi-Bellman(HJB) Equation, and prove that for general $L^p$ Physics-Informed Loss, a wide class of HJB equation is stable only if $p$ is sufficiently large. Therefore, the commonly used $L^2$ loss is not suitable for training PINN on those equations, while $L^{\infty}$ loss is a better choice. Based on the theoretical insight, we develop a novel PINN training algorithm to minimize the $L^{\infty}$ loss for HJB equations which is in a similar spirit to adversarial training. The effectiveness of the proposed algorithm is empirically demonstrated through experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge