Face processing emerges from object-trained convolutional neural networks

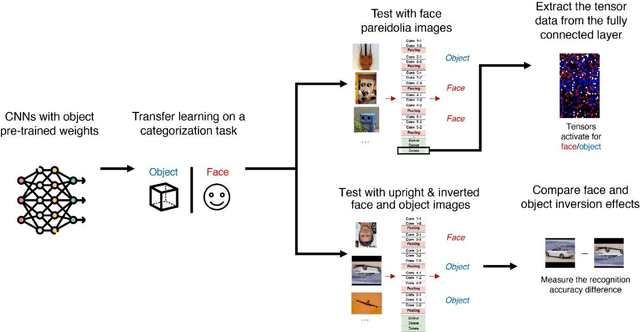
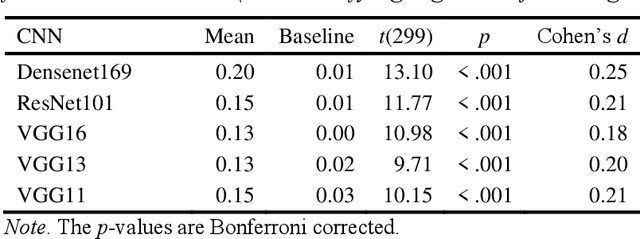
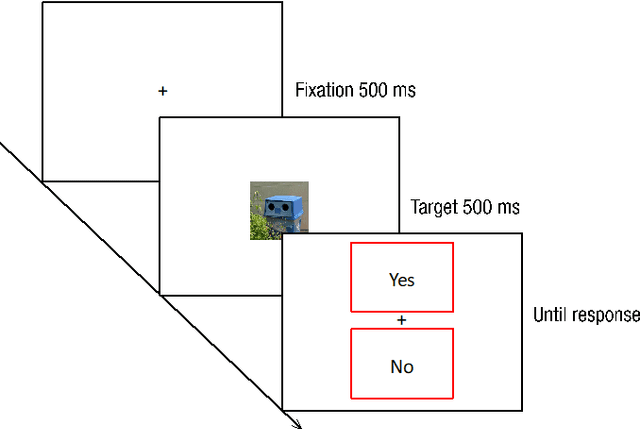
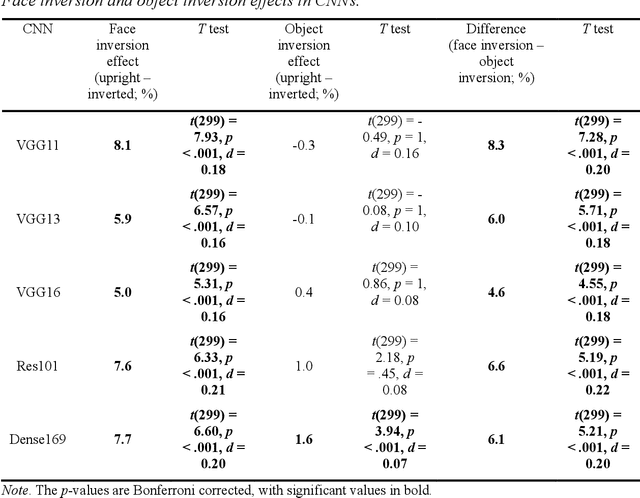
Whether face processing depends on unique, domain-specific neurocognitive mechanisms or domain-general object recognition mechanisms has long been debated. Directly testing these competing hypotheses in humans has proven challenging due to extensive exposure to both faces and objects. Here, we systematically test these hypotheses by capitalizing on recent progress in convolutional neural networks (CNNs) that can be trained without face exposure (i.e., pre-trained weights). Domain-general mechanism accounts posit that face processing can emerge from a neural network without specialized pre-training on faces. Consequently, we trained CNNs solely on objects and tested their ability to recognize and represent faces as well as objects that look like faces (face pareidolia stimuli).... Due to the character limits, for more details see in attached pdf

Forward Laplacian: A New Computational Framework for Neural Network-based Variational Monte Carlo

Neural network-based variational Monte Carlo (NN-VMC) has emerged as a promising cutting-edge technique of ab initio quantum chemistry. However, the high computational cost of existing approaches hinders their applications in realistic chemistry problems. Here, we report the development of a new NN-VMC method that achieves a remarkable speed-up by more than one order of magnitude, thereby greatly extending the applicability of NN-VMC to larger systems. Our key design is a novel computational framework named Forward Laplacian, which computes the Laplacian associated with neural networks, the bottleneck of NN-VMC, through an efficient forward propagation process. We then demonstrate that Forward Laplacian is not only versatile but also facilitates more developments of acceleration methods across various aspects, including optimization for sparse derivative matrix and efficient neural network design. Empirically, our approach enables NN-VMC to investigate a broader range of atoms, molecules and chemical reactions for the first time, providing valuable references to other ab initio methods. The results demonstrate a great potential in applying deep learning methods to solve general quantum mechanical problems.

TorchAudio: Building Blocks for Audio and Speech Processing

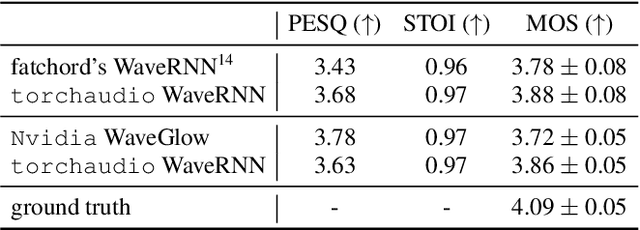
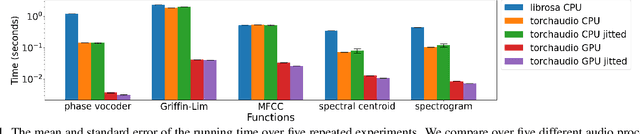
This document describes version 0.10 of torchaudio: building blocks for machine learning applications in the audio and speech processing domain. The objective of torchaudio is to accelerate the development and deployment of machine learning applications for researchers and engineers by providing off-the-shelf building blocks. The building blocks are designed to be GPU-compatible, automatically differentiable, and production-ready. torchaudio can be easily installed from Python Package Index repository and the source code is publicly available under a BSD-2-Clause License (as of September 2021) at https://github.com/pytorch/audio. In this document, we provide an overview of the design principles, functionalities, and benchmarks of torchaudio. We also benchmark our implementation of several audio and speech operations and models. We verify through the benchmarks that our implementations of various operations and models are valid and perform similarly to other publicly available implementations.

Learning Vision-based Reactive Policies for Obstacle Avoidance

In this paper, we address the problem of vision-based obstacle avoidance for robotic manipulators. This topic poses challenges for both perception and motion generation. While most work in the field aims at improving one of those aspects, we provide a unified framework for approaching this problem. The main goal of this framework is to connect perception and motion by identifying the relationship between the visual input and the corresponding motion representation. To this end, we propose a method for learning reactive obstacle avoidance policies. We evaluate our method on goal-reaching tasks for single and multiple obstacles scenarios. We show the ability of the proposed method to efficiently learn stable obstacle avoidance strategies at a high success rate, while maintaining closed-loop responsiveness required for critical applications like human-robot interaction.

Nonconvex Matrix Completion with Linearly Parameterized Factors

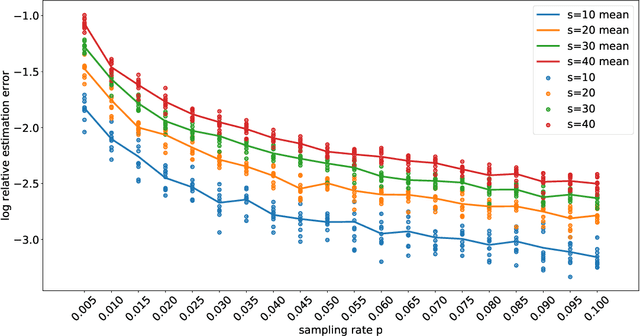
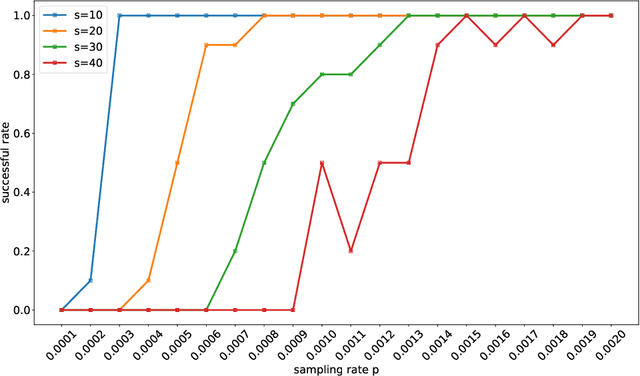
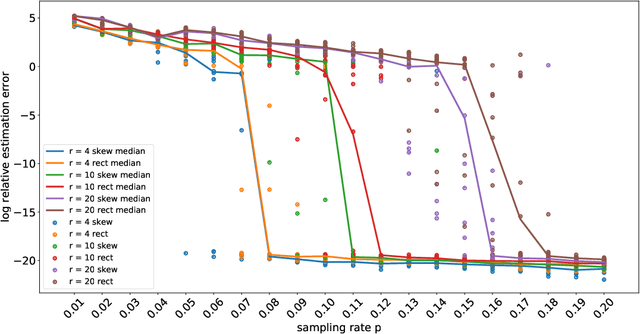
Techniques of matrix completion aim to impute a large portion of missing entries in a data matrix through a small portion of observed ones, with broad machine learning applications including collaborative filtering, pairwise ranking, etc. In practice, additional structures are usually employed in order to improve the accuracy of matrix completion. Examples include subspace constraints formed by side information in collaborative filtering, and skew symmetry in pairwise ranking. This paper performs a unified analysis of nonconvex matrix completion with linearly parameterized factorization, which covers the aforementioned examples as special cases. Importantly, uniform upper bounds for estimation errors are established for all local minima, provided that the sampling rate satisfies certain conditions determined by the rank, condition number, and incoherence parameter of the ground-truth low rank matrix. Empirical efficiency of the proposed method is further illustrated by numerical simulations.

Nonconvex Rectangular Matrix Completion via Gradient Descent without $\ell_{2,\infty}$ Regularization

The analysis of nonconvex matrix completion has recently attracted much attention in the community of machine learning thanks to its computational convenience. Existing analysis on this problem, however, usually relies on $\ell_{2,\infty}$ projection or regularization that involves unknown model parameters, although they are observed to be unnecessary in numerical simulations, see, e.g. Zheng and Lafferty [2016]. In this paper, we extend the analysis of the vanilla gradient descent for positive semidefinite matrix completion proposed in Ma et al. [2017] to the rectangular case, and more significantly, improve the required sampling complexity from $\widetilde{O}(r^3)$ to $\widetilde{O}(r^2)$. Our technical ideas and contributions are potentially useful in improving the leave-one-out analysis in other related problems.

Leveraging Elastic Demand for Forecasting

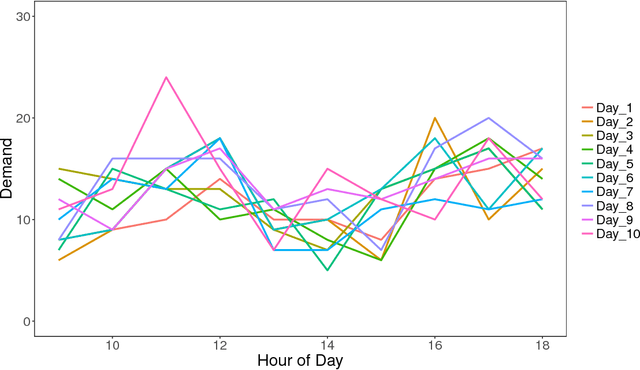
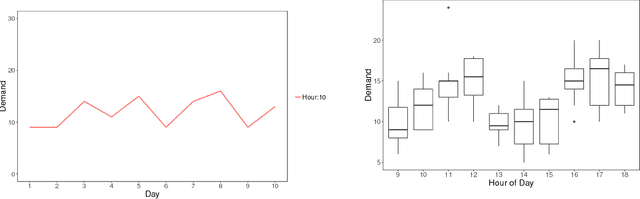
Demand variance can result in a mismatch between planned supply and actual demand. Demand shaping strategies such as pricing can be used to shift elastic demand to reduce the imbalance. In this work, we propose to consider elastic demand in the forecasting phase. We present a method to reallocate the historical elastic demand to reduce variance, thus making forecasting and supply planning more effective.

Memory-efficient Kernel PCA via Partial Matrix Sampling and Nonconvex Optimization: a Model-free Analysis of Local Minima

Kernel PCA is a widely used nonlinear dimension reduction technique in machine learning, but storing the kernel matrix is notoriously challenging when the sample size is large. Inspired by Yi et al. [2016], where the idea of partial matrix sampling followed by nonconvex optimization is proposed for matrix completion and robust PCA, we apply a similar approach to memory-efficient Kernel PCA. In theory, with no assumptions on the kernel matrix in terms of eigenvalues or eigenvectors, we established a model-free theory for the low-rank approximation based on any local minimum of the proposed objective function. As interesting byproducts, when the underlying positive semidefinite matrix is assumed to be low-rank and highly structured, corollaries of our main theorem improve the state-of-the-art results of Ge et al. [2016, 2017] for nonconvex matrix completion with no spurious local minima. Numerical experiments also show that our approach is competitive in terms of approximation accuracy compared to the well-known Nystr\"{o}m algorithm for Kernel PCA.