Nonconvex Matrix Completion with Linearly Parameterized Factors

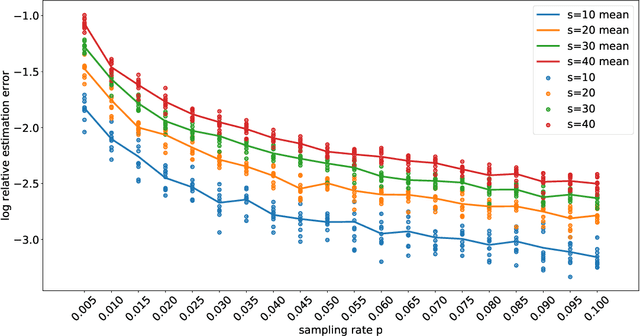
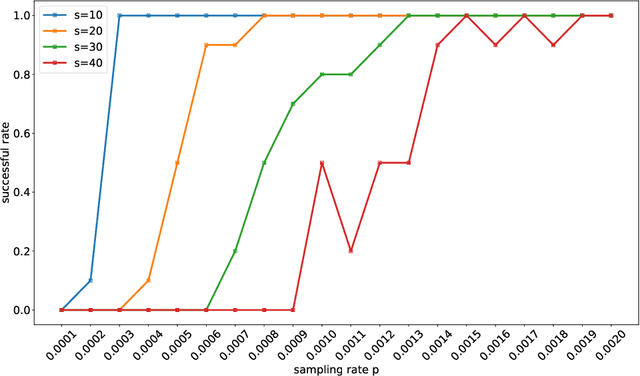
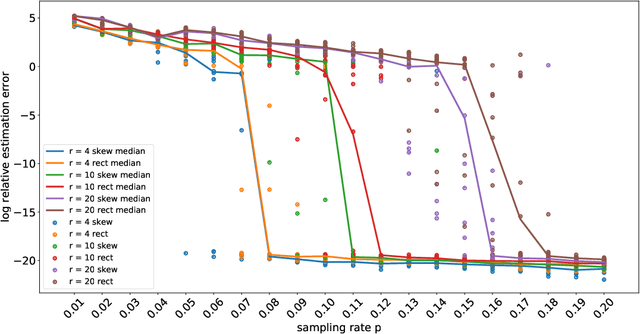
Techniques of matrix completion aim to impute a large portion of missing entries in a data matrix through a small portion of observed ones, with broad machine learning applications including collaborative filtering, pairwise ranking, etc. In practice, additional structures are usually employed in order to improve the accuracy of matrix completion. Examples include subspace constraints formed by side information in collaborative filtering, and skew symmetry in pairwise ranking. This paper performs a unified analysis of nonconvex matrix completion with linearly parameterized factorization, which covers the aforementioned examples as special cases. Importantly, uniform upper bounds for estimation errors are established for all local minima, provided that the sampling rate satisfies certain conditions determined by the rank, condition number, and incoherence parameter of the ground-truth low rank matrix. Empirical efficiency of the proposed method is further illustrated by numerical simulations.