Zongming Ma
Multi-modal contrastive learning adapts to intrinsic dimensions of shared latent variables
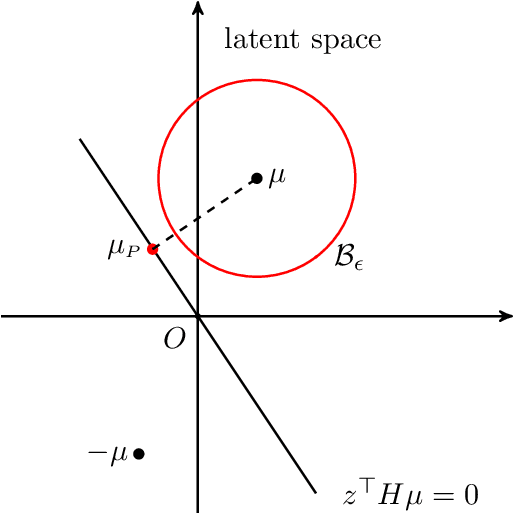
May 18, 2025Abstract:Multi-modal contrastive learning as a self-supervised representation learning technique has achieved great success in foundation model training, such as CLIP~\citep{radford2021learning}. In this paper, we study the theoretical properties of the learned representations from multi-modal contrastive learning beyond linear representations and specific data distributions. Our analysis reveals that, enabled by temperature optimization, multi-modal contrastive learning not only maximizes mutual information between modalities but also adapts to intrinsic dimensions of data, which can be much lower than user-specified dimensions for representation vectors. Experiments on both synthetic and real-world datasets demonstrate the ability of contrastive learning to learn low-dimensional and informative representations, bridging theoretical insights and practical performance.
One-Way Matching of Datasets with Low Rank Signals
Apr 29, 2022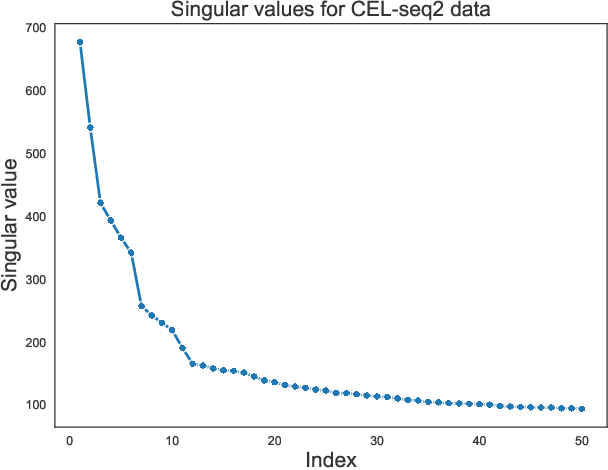
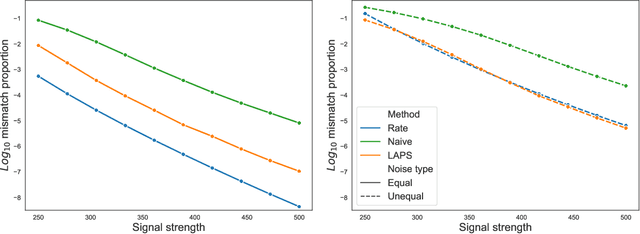

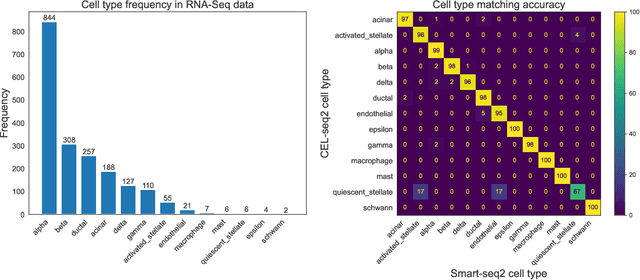
Abstract:We study one-way matching of a pair of datasets with low rank signals. Under a stylized model, we first derive information-theoretic limits of matching. We then show that linear assignment with projected data achieves fast rates of convergence and sometimes even minimax rate optimality for this task. The theoretical error bounds are corroborated by simulated examples. Furthermore, we illustrate practical use of the matching procedure on two single-cell data examples.
Sparse GCA and Thresholded Gradient Descent
Jul 01, 2021
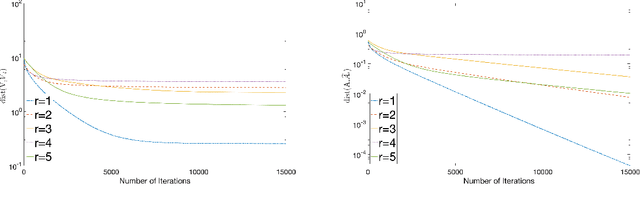


Abstract:Generalized correlation analysis (GCA) is concerned with uncovering linear relationships across multiple datasets. It generalizes canonical correlation analysis that is designed for two datasets. We study sparse GCA when there are potentially multiple generalized correlation tuples in data and the loading matrix has a small number of nonzero rows. It includes sparse CCA and sparse PCA of correlation matrices as special cases. We first formulate sparse GCA as generalized eigenvalue problems at both population and sample levels via a careful choice of normalization constraints. Based on a Lagrangian form of the sample optimization problem, we propose a thresholded gradient descent algorithm for estimating GCA loading vectors and matrices in high dimensions. We derive tight estimation error bounds for estimators generated by the algorithm with proper initialization. We also demonstrate the prowess of the algorithm on a number of synthetic datasets.
Global and Individualized Community Detection in Inhomogeneous Multilayer Networks
Dec 02, 2020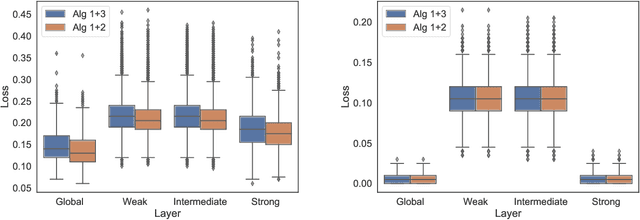
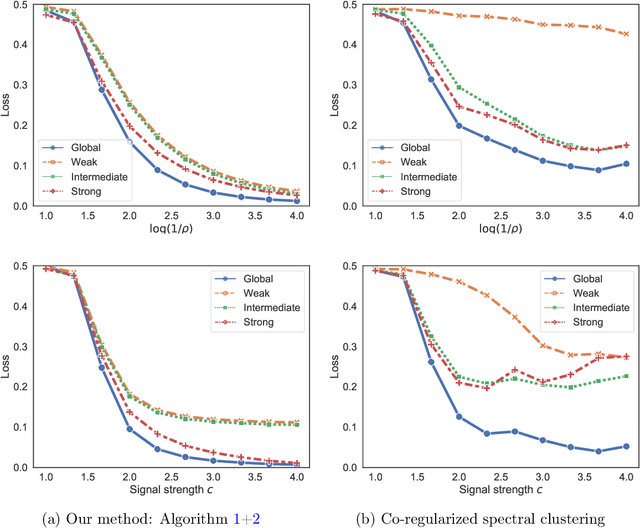
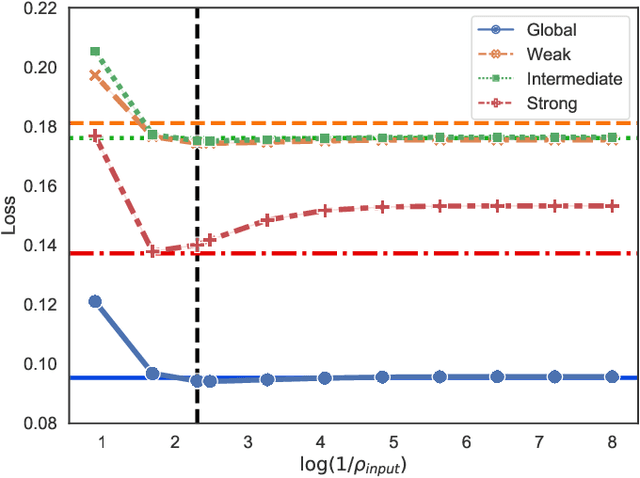
Abstract:In network applications, it has become increasingly common to obtain datasets in the form of multiple networks observed on the same set of subjects, where each network is obtained in a related but different experiment condition or application scenario. Such datasets can be modeled by multilayer networks where each layer is a separate network itself while different layers are associated and share some common information. The present paper studies community detection in a stylized yet informative inhomogeneous multilayer network model. In our model, layers are generated by different stochastic block models, the community structures of which are (random) perturbations of a common global structure while the connecting probabilities in different layers are not related. Focusing on the symmetric two block case, we establish minimax rates for both \emph{global estimation} of the common structure and \emph{individualized estimation} of layer-wise community structures. Both minimax rates have sharp exponents. In addition, we provide an efficient algorithm that is simultaneously asymptotic minimax optimal for both estimation tasks under mild conditions. The optimal rates depend on the \emph{parity} of the number of most informative layers, a phenomenon that is caused by inhomogeneity across layers.
Community detection in sparse latent space models
Aug 04, 2020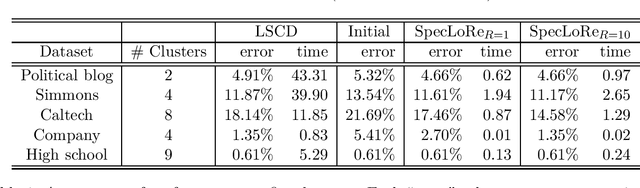

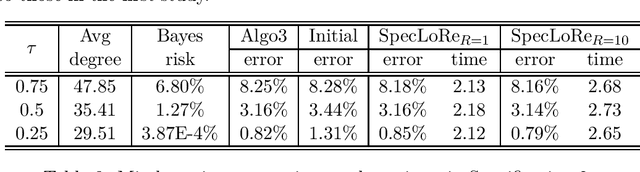
Abstract:We show that a simple community detection algorithm originated from stochastic blockmodel literature achieves consistency, and even optimality, for a broad and flexible class of sparse latent space models. The class of models includes latent eigenmodels (arXiv:0711.1146). The community detection algorithm is based on spectral clustering followed by local refinement via normalized edge counting.
Nonconvex Matrix Completion with Linearly Parameterized Factors
Mar 29, 2020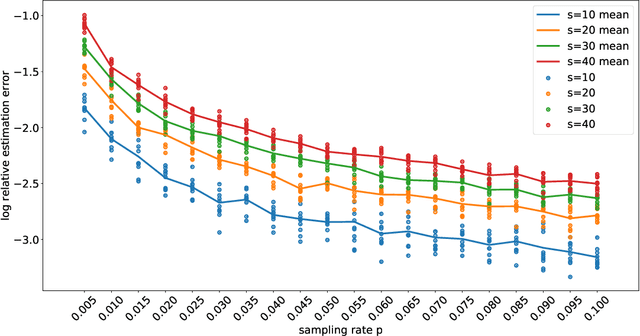
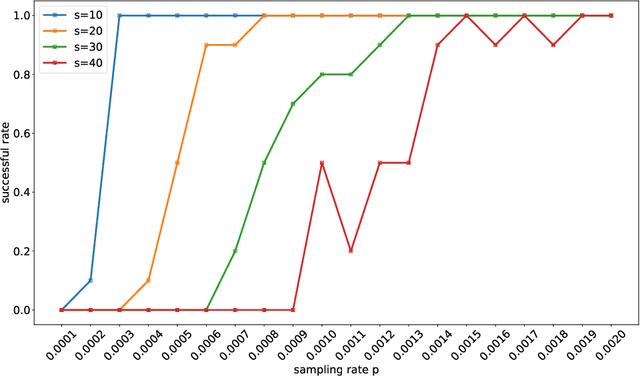
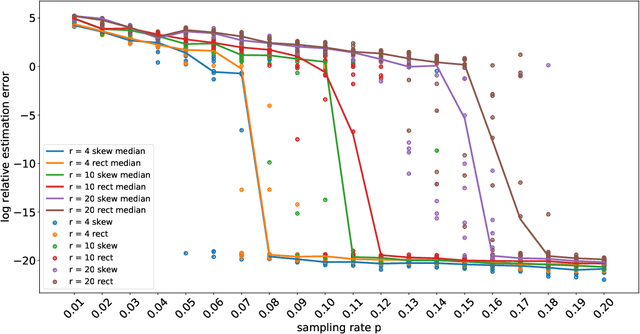
Abstract:Techniques of matrix completion aim to impute a large portion of missing entries in a data matrix through a small portion of observed ones, with broad machine learning applications including collaborative filtering, pairwise ranking, etc. In practice, additional structures are usually employed in order to improve the accuracy of matrix completion. Examples include subspace constraints formed by side information in collaborative filtering, and skew symmetry in pairwise ranking. This paper performs a unified analysis of nonconvex matrix completion with linearly parameterized factorization, which covers the aforementioned examples as special cases. Importantly, uniform upper bounds for estimation errors are established for all local minima, provided that the sampling rate satisfies certain conditions determined by the rank, condition number, and incoherence parameter of the ground-truth low rank matrix. Empirical efficiency of the proposed method is further illustrated by numerical simulations.
Efficient random graph matching via degree profiles
Nov 19, 2018
Abstract:Random graph matching refers to recovering the underlying vertex correspondence between two random graphs with correlated edges; a prominent example is when the two random graphs are given by Erd\H{o}s-R\'{e}nyi graphs $G(n,\frac{d}{n})$. This can be viewed as an average-case and noisy version of the graph isomorphism problem. Under this model, the maximum likelihood estimator is equivalent to solving the intractable quadratic assignment problem. This work develops an $\tilde{O}(n d^2+n^2)$-time algorithm which perfectly recovers the true vertex correspondence with high probability, provided that the average degree is at least $d = \Omega(\log^2 n)$ and the two graphs differ by at most $\delta = O( \log^{-2}(n) )$ fraction of edges. For dense graphs and sparse graphs, this can be improved to $\delta = O( \log^{-2/3}(n) )$ and $\delta = O( \log^{-2}(d) )$ respectively, both in polynomial time. The methodology is based on appropriately chosen distance statistics of the degree profiles (empirical distribution of the degrees of neighbors). Before this work, the best known result achieves $\delta=O(1)$ and $n^{o(1)} \leq d \leq n^c$ for some constant $c$ with an $n^{O(\log n)}$-time algorithm \cite{barak2018nearly} and $\delta=\tilde O((d/n)^4)$ and $d = \tilde{\Omega}(n^{4/5})$ with a polynomial-time algorithm \cite{dai2018performance}.
Minimax Rates in Network Analysis: Graphon Estimation, Community Detection and Hypothesis Testing
Nov 14, 2018
Abstract:This paper surveys some recent developments in fundamental limits and optimal algorithms for network analysis. We focus on minimax optimal rates in three fundamental problems of network analysis: graphon estimation, community detection, and hypothesis testing. For each problem, we review state-of-the-art results in the literature followed by general principles behind the optimal procedures that lead to minimax estimation and testing. This allows us to connect problems in network analysis to other statistical inference problems from a general perspective.
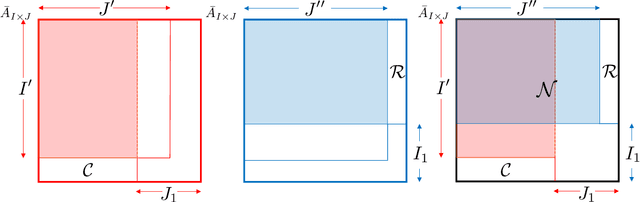
Optimal Estimation and Completion of Matrices with Biclustering Structures
Oct 22, 2018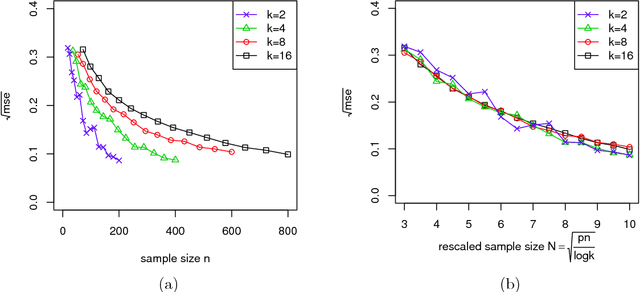
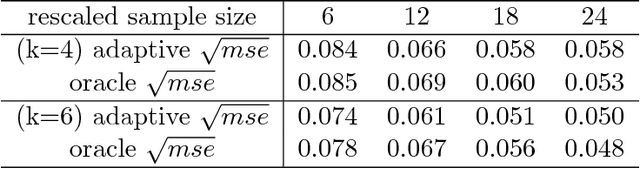
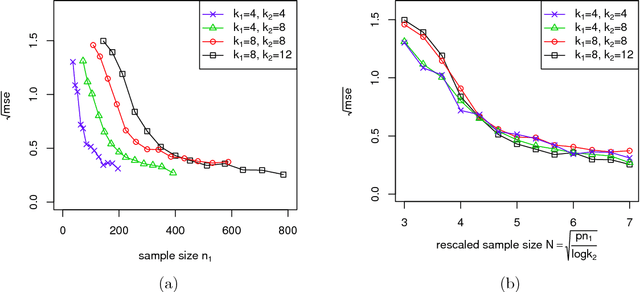
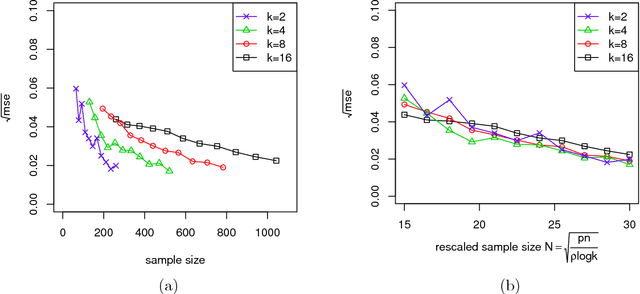
Abstract:Biclustering structures in data matrices were first formalized in a seminal paper by John Hartigan (1972) where one seeks to cluster cases and variables simultaneously. Such structures are also prevalent in block modeling of networks. In this paper, we develop a unified theory for the estimation and completion of matrices with biclustering structures, where the data is a partially observed and noise contaminated data matrix with a certain biclustering structure. In particular, we show that a constrained least squares estimator achieves minimax rate-optimal performance in several of the most important scenarios. To this end, we derive unified high probability upper bounds for all sub-Gaussian data and also provide matching minimax lower bounds in both Gaussian and binary cases. Due to the close connection of graphon to stochastic block models, an immediate consequence of our general results is a minimax rate-optimal estimator for sparse graphons.
Exploration of Large Networks with Covariates via Fast and Universal Latent Space Model Fitting
Aug 18, 2017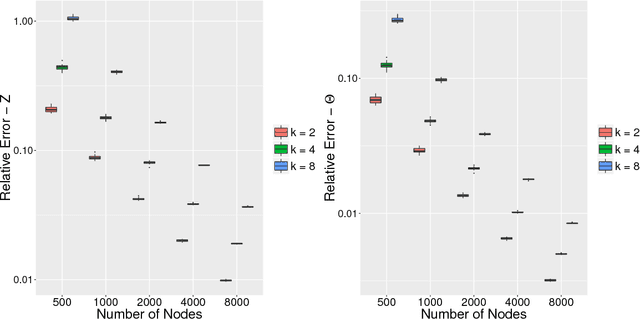

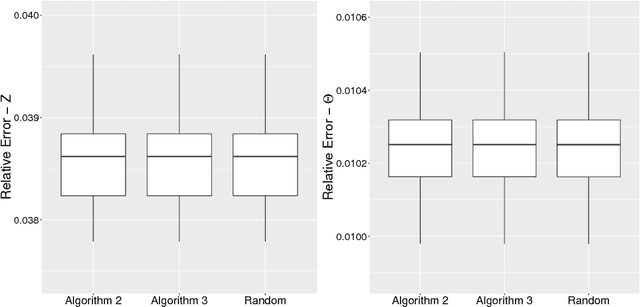
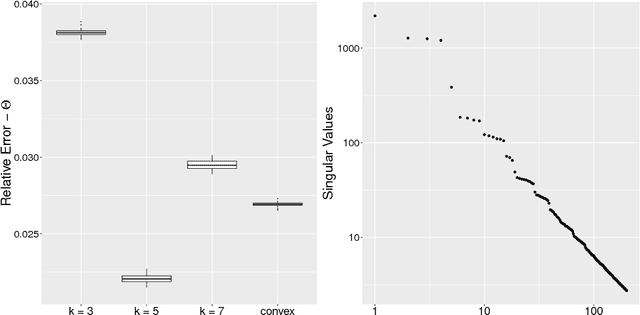
Abstract:Latent space models are effective tools for statistical modeling and exploration of network data. These models can effectively model real world network characteristics such as degree heterogeneity, transitivity, homophily, etc. Due to their close connection to generalized linear models, it is also natural to incorporate covariate information in them. The current paper presents two universal fitting algorithms for networks with edge covariates: one based on nuclear norm penalization and the other based on projected gradient descent. Both algorithms are motivated by maximizing likelihood for a special class of inner-product models while working simultaneously for a wide range of different latent space models, such as distance models, which allow latent vectors to affect edge formation in flexible ways. These fitting methods, especially the one based on projected gradient descent, are fast and scalable to large networks. We obtain their rates of convergence for both inner-product models and beyond. The effectiveness of the modeling approach and fitting algorithms is demonstrated on five real world network datasets for different statistical tasks, including community detection with and without edge covariates, and network assisted learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge