Global and Individualized Community Detection in Inhomogeneous Multilayer Networks
Paper and Code
Dec 02, 2020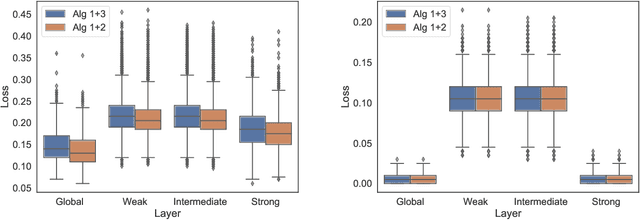
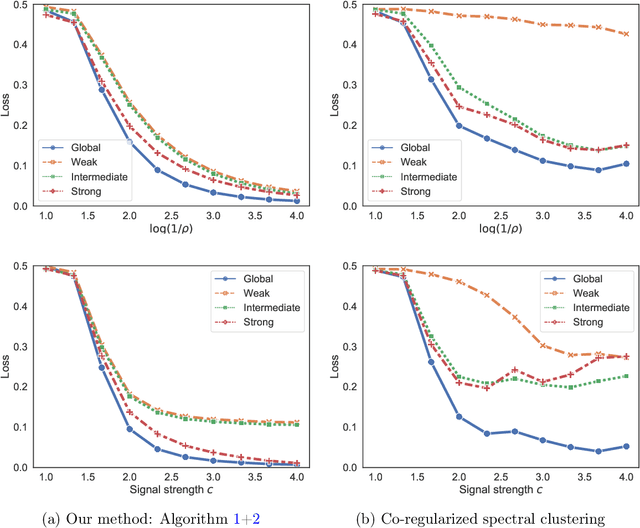
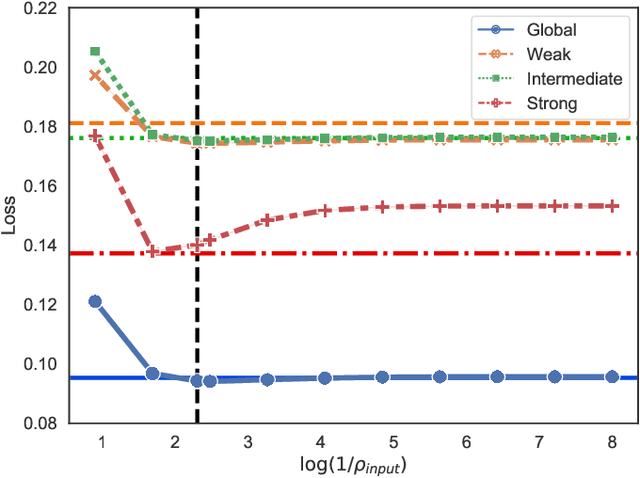
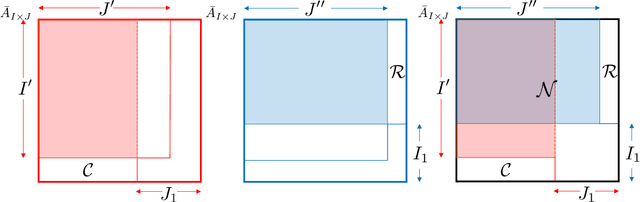
In network applications, it has become increasingly common to obtain datasets in the form of multiple networks observed on the same set of subjects, where each network is obtained in a related but different experiment condition or application scenario. Such datasets can be modeled by multilayer networks where each layer is a separate network itself while different layers are associated and share some common information. The present paper studies community detection in a stylized yet informative inhomogeneous multilayer network model. In our model, layers are generated by different stochastic block models, the community structures of which are (random) perturbations of a common global structure while the connecting probabilities in different layers are not related. Focusing on the symmetric two block case, we establish minimax rates for both \emph{global estimation} of the common structure and \emph{individualized estimation} of layer-wise community structures. Both minimax rates have sharp exponents. In addition, we provide an efficient algorithm that is simultaneously asymptotic minimax optimal for both estimation tasks under mild conditions. The optimal rates depend on the \emph{parity} of the number of most informative layers, a phenomenon that is caused by inhomogeneity across layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge