NeuroGauss4D-PCI: 4D Neural Fields and Gaussian Deformation Fields for Point Cloud Interpolation

Point Cloud Interpolation confronts challenges from point sparsity, complex spatiotemporal dynamics, and the difficulty of deriving complete 3D point clouds from sparse temporal information. This paper presents NeuroGauss4D-PCI, which excels at modeling complex non-rigid deformations across varied dynamic scenes. The method begins with an iterative Gaussian cloud soft clustering module, offering structured temporal point cloud representations. The proposed temporal radial basis function Gaussian residual utilizes Gaussian parameter interpolation over time, enabling smooth parameter transitions and capturing temporal residuals of Gaussian distributions. Additionally, a 4D Gaussian deformation field tracks the evolution of these parameters, creating continuous spatiotemporal deformation fields. A 4D neural field transforms low-dimensional spatiotemporal coordinates ($x,y,z,t$) into a high-dimensional latent space. Finally, we adaptively and efficiently fuse the latent features from neural fields and the geometric features from Gaussian deformation fields. NeuroGauss4D-PCI outperforms existing methods in point cloud frame interpolation, delivering leading performance on both object-level (DHB) and large-scale autonomous driving datasets (NL-Drive), with scalability to auto-labeling and point cloud densification tasks. The source code is released at https://github.com/jiangchaokang/NeuroGauss4D-PCI.

3DSFLabelling: Boosting 3D Scene Flow Estimation by Pseudo Auto-labelling

Learning 3D scene flow from LiDAR point clouds presents significant difficulties, including poor generalization from synthetic datasets to real scenes, scarcity of real-world 3D labels, and poor performance on real sparse LiDAR point clouds. We present a novel approach from the perspective of auto-labelling, aiming to generate a large number of 3D scene flow pseudo labels for real-world LiDAR point clouds. Specifically, we employ the assumption of rigid body motion to simulate potential object-level rigid movements in autonomous driving scenarios. By updating different motion attributes for multiple anchor boxes, the rigid motion decomposition is obtained for the whole scene. Furthermore, we developed a novel 3D scene flow data augmentation method for global and local motion. By perfectly synthesizing target point clouds based on augmented motion parameters, we easily obtain lots of 3D scene flow labels in point clouds highly consistent with real scenarios. On multiple real-world datasets including LiDAR KITTI, nuScenes, and Argoverse, our method outperforms all previous supervised and unsupervised methods without requiring manual labelling. Impressively, our method achieves a tenfold reduction in EPE3D metric on the LiDAR KITTI dataset, reducing it from $0.190m$ to a mere $0.008m$ error.

GEDepth: Ground Embedding for Monocular Depth Estimation

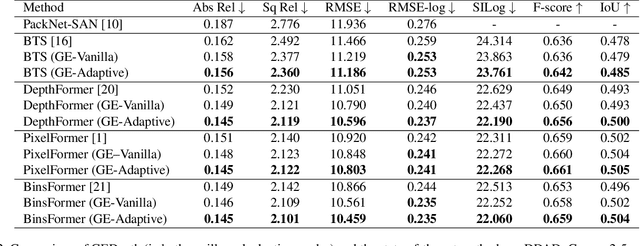
Monocular depth estimation is an ill-posed problem as the same 2D image can be projected from infinite 3D scenes. Although the leading algorithms in this field have reported significant improvement, they are essentially geared to the particular compound of pictorial observations and camera parameters (i.e., intrinsics and extrinsics), strongly limiting their generalizability in real-world scenarios. To cope with this challenge, this paper proposes a novel ground embedding module to decouple camera parameters from pictorial cues, thus promoting the generalization capability. Given camera parameters, the proposed module generates the ground depth, which is stacked with the input image and referenced in the final depth prediction. A ground attention is designed in the module to optimally combine ground depth with residual depth. Our ground embedding is highly flexible and lightweight, leading to a plug-in module that is amenable to be integrated into various depth estimation networks. Experiments reveal that our approach achieves the state-of-the-art results on popular benchmarks, and more importantly, renders significant generalization improvement on a wide range of cross-domain tests.

hBert + BiasCorp -- Fighting Racism on the Web

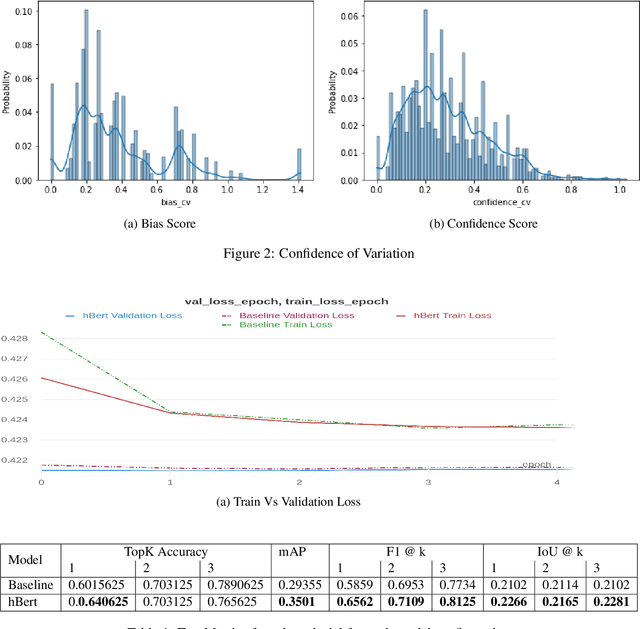
Subtle and overt racism is still present both in physical and online communities today and has impacted many lives in different segments of the society. In this short piece of work, we present how we're tackling this societal issue with Natural Language Processing. We are releasing BiasCorp, a dataset containing 139,090 comments and news segment from three specific sources - Fox News, BreitbartNews and YouTube. The first batch (45,000 manually annotated) is ready for publication. We are currently in the final phase of manually labeling the remaining dataset using Amazon Mechanical Turk. BERT has been used widely in several downstream tasks. In this work, we present hBERT, where we modify certain layers of the pretrained BERT model with the new Hopfield Layer. hBert generalizes well across different distributions with the added advantage of a reduced model complexity. We are also releasing a JavaScript library and a Chrome Extension Application, to help developers make use of our trained model in web applications (say chat application) and for users to identify and report racially biased contents on the web respectively.

Noise Contrastive Estimation and Negative Sampling for Conditional Models: Consistency and Statistical Efficiency

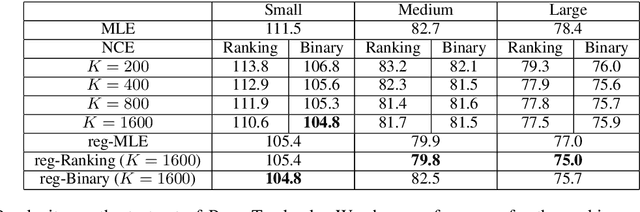
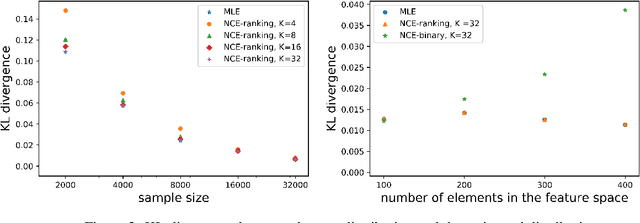
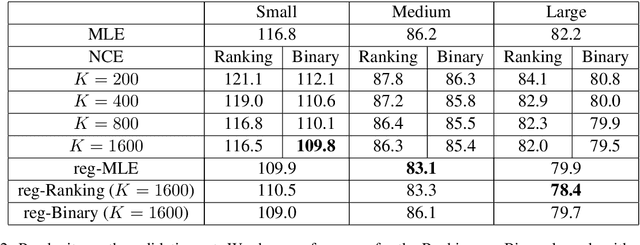
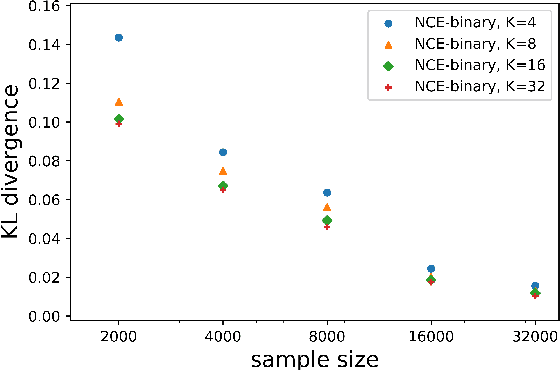
Noise Contrastive Estimation (NCE) is a powerful parameter estimation method for log-linear models, which avoids calculation of the partition function or its derivatives at each training step, a computationally demanding step in many cases. It is closely related to negative sampling methods, now widely used in NLP. This paper considers NCE-based estimation of conditional models. Conditional models are frequently encountered in practice; however there has not been a rigorous theoretical analysis of NCE in this setting, and we will argue there are subtle but important questions when generalizing NCE to the conditional case. In particular, we analyze two variants of NCE for conditional models: one based on a classification objective, the other based on a ranking objective. We show that the ranking-based variant of NCE gives consistent parameter estimates under weaker assumptions than the classification-based method; we analyze the statistical efficiency of the ranking-based and classification-based variants of NCE; finally we describe experiments on synthetic data and language modeling showing the effectiveness and trade-offs of both methods.

Subspace Perspective on Canonical Correlation Analysis: Dimension Reduction and Minimax Rates

Canonical correlation analysis (CCA) is a fundamental statistical tool for exploring the correlation structure between two sets of random variables. In this paper, motivated by recent success of applying CCA to learn low dimensional representations of high dimensional objects, we propose to quantify the estimation loss of CCA by the excess prediction loss defined through a prediction-after-dimension-reduction framework. Such framework suggests viewing CCA estimation as estimating the subspaces spanned by the canonical variates. Interestedly, the proposed error metrics derived from the excess prediction loss turn out to be closely related to the principal angles between the subspaces spanned by the population and sample canonical variates respectively. We characterize the non-asymptotic minimax rates under the proposed metrics, especially the dependency of the minimax rates on the key quantities including the dimensions, the condition number of the covariance matrices, the canonical correlations and the eigen-gap, with minimal assumptions on the joint covariance matrix. To the best of our knowledge, this is the first finite sample result that captures the effect of the canonical correlations on the minimax rates.

Exploration of Large Networks with Covariates via Fast and Universal Latent Space Model Fitting

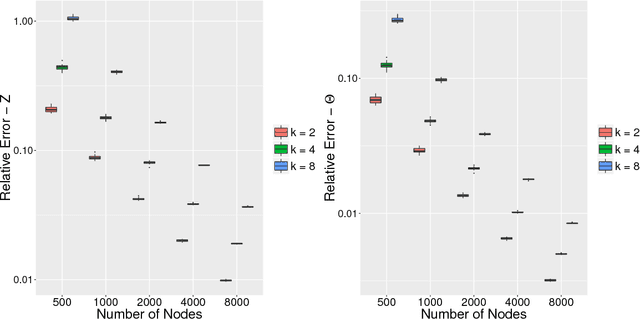
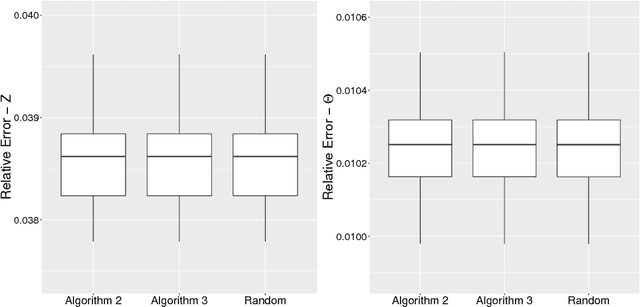
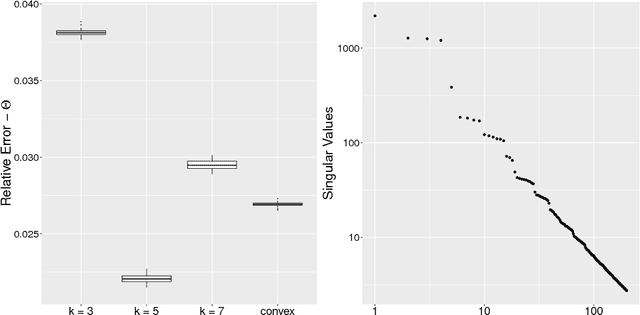
Latent space models are effective tools for statistical modeling and exploration of network data. These models can effectively model real world network characteristics such as degree heterogeneity, transitivity, homophily, etc. Due to their close connection to generalized linear models, it is also natural to incorporate covariate information in them. The current paper presents two universal fitting algorithms for networks with edge covariates: one based on nuclear norm penalization and the other based on projected gradient descent. Both algorithms are motivated by maximizing likelihood for a special class of inner-product models while working simultaneously for a wide range of different latent space models, such as distance models, which allow latent vectors to affect edge formation in flexible ways. These fitting methods, especially the one based on projected gradient descent, are fast and scalable to large networks. We obtain their rates of convergence for both inner-product models and beyond. The effectiveness of the modeling approach and fitting algorithms is demonstrated on five real world network datasets for different statistical tasks, including community detection with and without edge covariates, and network assisted learning.

Finding Linear Structure in Large Datasets with Scalable Canonical Correlation Analysis

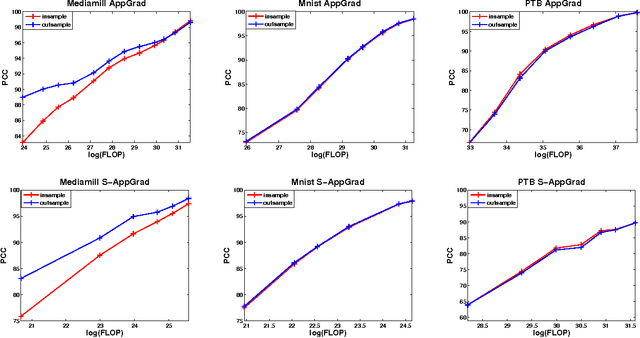
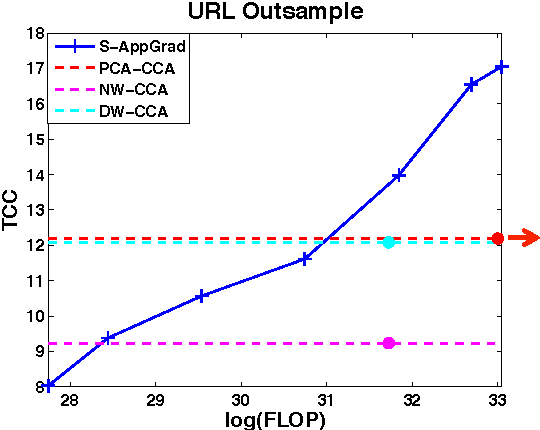
Canonical Correlation Analysis (CCA) is a widely used spectral technique for finding correlation structures in multi-view datasets. In this paper, we tackle the problem of large scale CCA, where classical algorithms, usually requiring computing the product of two huge matrices and huge matrix decomposition, are computationally and storage expensive. We recast CCA from a novel perspective and propose a scalable and memory efficient Augmented Approximate Gradient (AppGrad) scheme for finding top $k$ dimensional canonical subspace which only involves large matrix multiplying a thin matrix of width $k$ and small matrix decomposition of dimension $k\times k$. Further, AppGrad achieves optimal storage complexity $O(k(p_1+p_2))$, compared with classical algorithms which usually require $O(p_1^2+p_2^2)$ space to store two dense whitening matrices. The proposed scheme naturally generalizes to stochastic optimization regime, especially efficient for huge datasets where batch algorithms are prohibitive. The online property of stochastic AppGrad is also well suited to the streaming scenario, where data comes sequentially. To the best of our knowledge, it is the first stochastic algorithm for CCA. Experiments on four real data sets are provided to show the effectiveness of the proposed methods.