One-Way Matching of Datasets with Low Rank Signals
Paper and Code
Apr 29, 2022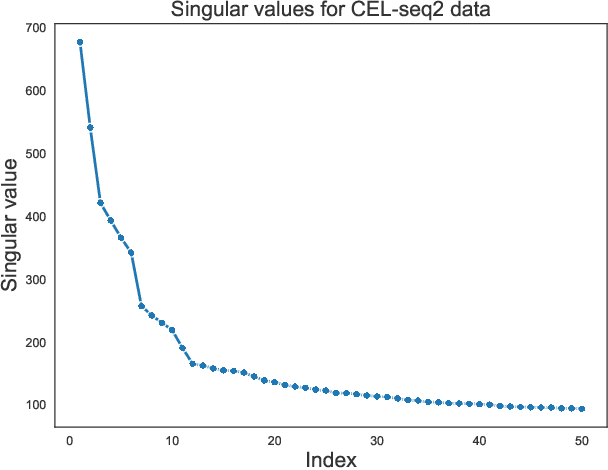
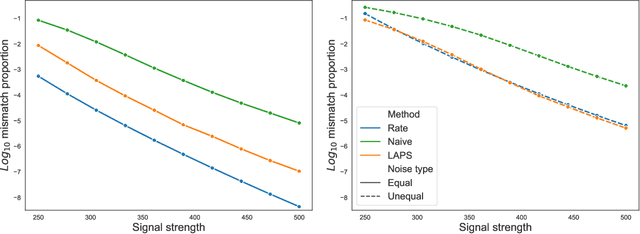

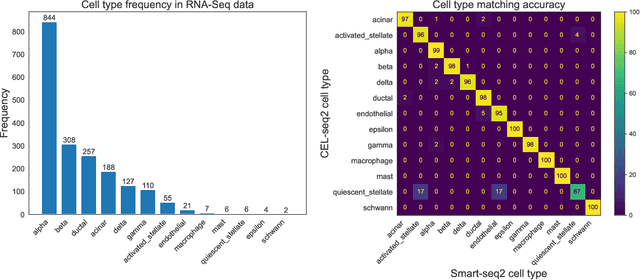
We study one-way matching of a pair of datasets with low rank signals. Under a stylized model, we first derive information-theoretic limits of matching. We then show that linear assignment with projected data achieves fast rates of convergence and sometimes even minimax rate optimality for this task. The theoretical error bounds are corroborated by simulated examples. Furthermore, we illustrate practical use of the matching procedure on two single-cell data examples.
* 64 pages, 7 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge