Efficient random graph matching via degree profiles
Paper and Code
Nov 19, 2018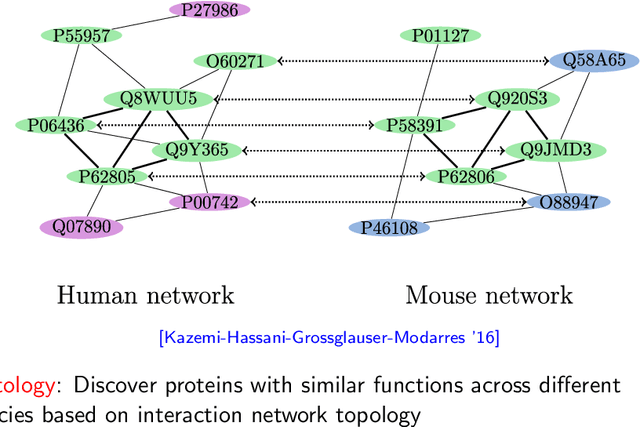
Random graph matching refers to recovering the underlying vertex correspondence between two random graphs with correlated edges; a prominent example is when the two random graphs are given by Erd\H{o}s-R\'{e}nyi graphs $G(n,\frac{d}{n})$. This can be viewed as an average-case and noisy version of the graph isomorphism problem. Under this model, the maximum likelihood estimator is equivalent to solving the intractable quadratic assignment problem. This work develops an $\tilde{O}(n d^2+n^2)$-time algorithm which perfectly recovers the true vertex correspondence with high probability, provided that the average degree is at least $d = \Omega(\log^2 n)$ and the two graphs differ by at most $\delta = O( \log^{-2}(n) )$ fraction of edges. For dense graphs and sparse graphs, this can be improved to $\delta = O( \log^{-2/3}(n) )$ and $\delta = O( \log^{-2}(d) )$ respectively, both in polynomial time. The methodology is based on appropriately chosen distance statistics of the degree profiles (empirical distribution of the degrees of neighbors). Before this work, the best known result achieves $\delta=O(1)$ and $n^{o(1)} \leq d \leq n^c$ for some constant $c$ with an $n^{O(\log n)}$-time algorithm \cite{barak2018nearly} and $\delta=\tilde O((d/n)^4)$ and $d = \tilde{\Omega}(n^{4/5})$ with a polynomial-time algorithm \cite{dai2018performance}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge