EquiReg: Equivariance Regularized Diffusion for Inverse Problems

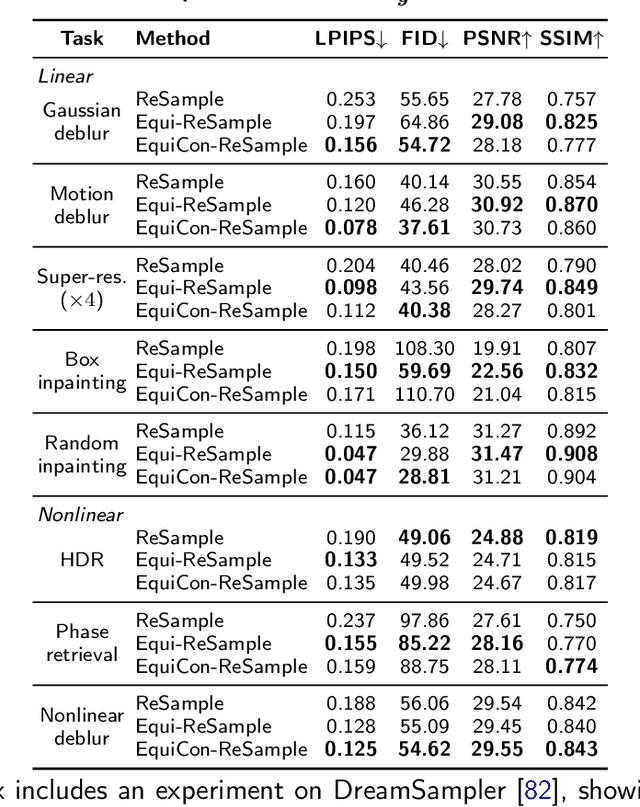
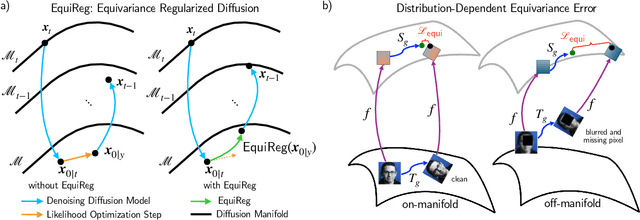
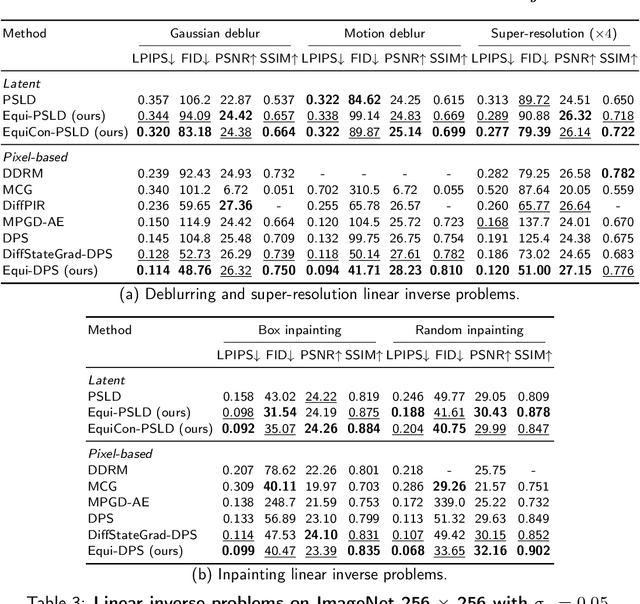
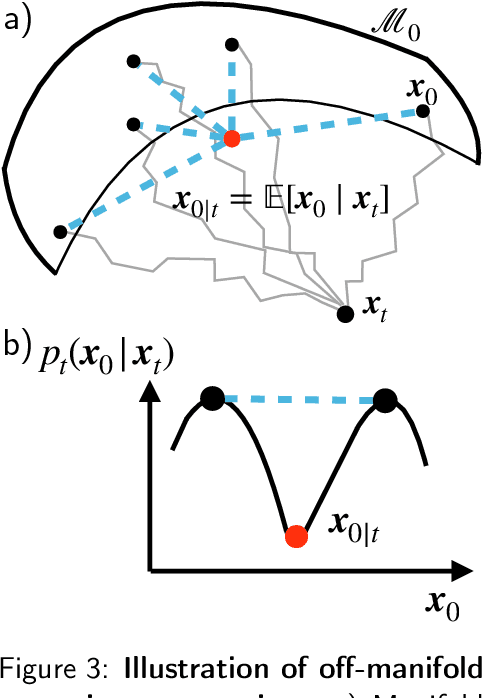
Diffusion models represent the state-of-the-art for solving inverse problems such as image restoration tasks. In the Bayesian framework, diffusion-based inverse solvers incorporate a likelihood term to guide the prior sampling process, generating data consistent with the posterior distribution. However, due to the intractability of the likelihood term, many current methods rely on isotropic Gaussian approximations, which lead to deviations from the data manifold and result in inconsistent, unstable reconstructions. We propose Equivariance Regularized (EquiReg) diffusion, a general framework for regularizing posterior sampling in diffusion-based inverse problem solvers. EquiReg enhances reconstructions by reweighting diffusion trajectories and penalizing those that deviate from the data manifold. We define a new distribution-dependent equivariance error, empirically identify functions that exhibit low error for on-manifold samples and higher error for off-manifold samples, and leverage these functions to regularize the diffusion sampling process. When applied to a variety of solvers, EquiReg outperforms state-of-the-art diffusion models in both linear and nonlinear image restoration tasks, as well as in reconstructing partial differential equations.

Guided Diffusion Sampling on Function Spaces with Applications to PDEs

We propose a general framework for conditional sampling in PDE-based inverse problems, targeting the recovery of whole solutions from extremely sparse or noisy measurements. This is accomplished by a function-space diffusion model and plug-and-play guidance for conditioning. Our method first trains an unconditional discretization-agnostic denoising model using neural operator architectures. At inference, we refine the samples to satisfy sparse observation data via a gradient-based guidance mechanism. Through rigorous mathematical analysis, we extend Tweedie's formula to infinite-dimensional Hilbert spaces, providing the theoretical foundation for our posterior sampling approach. Our method (FunDPS) accurately captures posterior distributions in function spaces under minimal supervision and severe data scarcity. Across five PDE tasks with only 3% observation, our method achieves an average 32% accuracy improvement over state-of-the-art fixed-resolution diffusion baselines while reducing sampling steps by 4x. Furthermore, multi-resolution fine-tuning ensures strong cross-resolution generalizability. To the best of our knowledge, this is the first diffusion-based framework to operate independently of discretization, offering a practical and flexible solution for forward and inverse problems in the context of PDEs. Code is available at https://github.com/neuraloperator/FunDPS

Adversarial Vessel-Unveiling Semi-Supervised Segmentation for Retinopathy of Prematurity Diagnosis

Accurate segmentation of retinal images plays a crucial role in aiding ophthalmologists in diagnosing retinopathy of prematurity (ROP) and assessing its severity. However, due to their underdeveloped, thinner vessels, manual annotation in infant fundus images is very complex, and this presents challenges for fully supervised learning. To address the scarcity of annotations, we propose a semi supervised segmentation framework designed to advance ROP studies without the need for extensive manual vessel annotation. Unlike previous methods that rely solely on limited labeled data, our approach leverages teacher student learning by integrating two powerful components: an uncertainty weighted vessel unveiling module and domain adversarial learning. The vessel unveiling module helps the model effectively reveal obscured and hard to detect vessel structures, while adversarial training aligns feature representations across different domains, ensuring robust and generalizable vessel segmentations. We validate our approach on public datasets (CHASEDB, STARE) and an in-house ROP dataset, demonstrating its superior performance across multiple evaluation metrics. Additionally, we extend the model's utility to a downstream task of ROP multi-stage classification, where vessel masks extracted by our segmentation model improve diagnostic accuracy. The promising results in classification underscore the model's potential for clinical application, particularly in early-stage ROP diagnosis and intervention. Overall, our work offers a scalable solution for leveraging unlabeled data in pediatric ophthalmology, opening new avenues for biomarker discovery and clinical research.

A Theoretical Study of Neural Network Expressive Power via Manifold Topology

A prevalent assumption regarding real-world data is that it lies on or close to a low-dimensional manifold. When deploying a neural network on data manifolds, the required size, i.e., the number of neurons of the network, heavily depends on the intricacy of the underlying latent manifold. While significant advancements have been made in understanding the geometric attributes of manifolds, it's essential to recognize that topology, too, is a fundamental characteristic of manifolds. In this study, we investigate network expressive power in terms of the latent data manifold. Integrating both topological and geometric facets of the data manifold, we present a size upper bound of ReLU neural networks.

Backdooring Vision-Language Models with Out-Of-Distribution Data

The emergence of Vision-Language Models (VLMs) represents a significant advancement in integrating computer vision with Large Language Models (LLMs) to generate detailed text descriptions from visual inputs. Despite their growing importance, the security of VLMs, particularly against backdoor attacks, is under explored. Moreover, prior works often assume attackers have access to the original training data, which is often unrealistic. In this paper, we address a more practical and challenging scenario where attackers must rely solely on Out-Of-Distribution (OOD) data. We introduce VLOOD (Backdooring Vision-Language Models with Out-of-Distribution Data), a novel approach with two key contributions: (1) demonstrating backdoor attacks on VLMs in complex image-to-text tasks while minimizing degradation of the original semantics under poisoned inputs, and (2) proposing innovative techniques for backdoor injection without requiring any access to the original training data. Our evaluation on image captioning and visual question answering (VQA) tasks confirms the effectiveness of VLOOD, revealing a critical security vulnerability in VLMs and laying the foundation for future research on securing multimodal models against sophisticated threats.

Topological Analysis of Mouse Brain Vasculature via 3D Light-sheet Microscopy Images

Vascular networks play a crucial role in understanding brain functionalities. Brain integrity and function, neuronal activity and plasticity, which are crucial for learning, are actively modulated by their local environments, specifically vascular networks. With recent developments in high-resolution 3D light-sheet microscopy imaging together with tissue processing techniques, it becomes feasible to obtain and examine large-scale brain vasculature in mice. To establish a structural foundation for functional study, however, we need advanced image analysis and structural modeling methods. Existing works use geometric features such as thickness, tortuosity, etc. However, geometric features cannot fully capture structural characteristics such as the richness of branches, connectivity, etc. In this paper, we study the morphology of brain vasculature through a topological lens. We extract topological features based on the theory of topological data analysis. Comparing of these robust and multi-scale topological structural features across different brain anatomical structures and between normal and obese populations sheds light on their promising future in studying neurological diseases.

Preconditioning for Physics-Informed Neural Networks

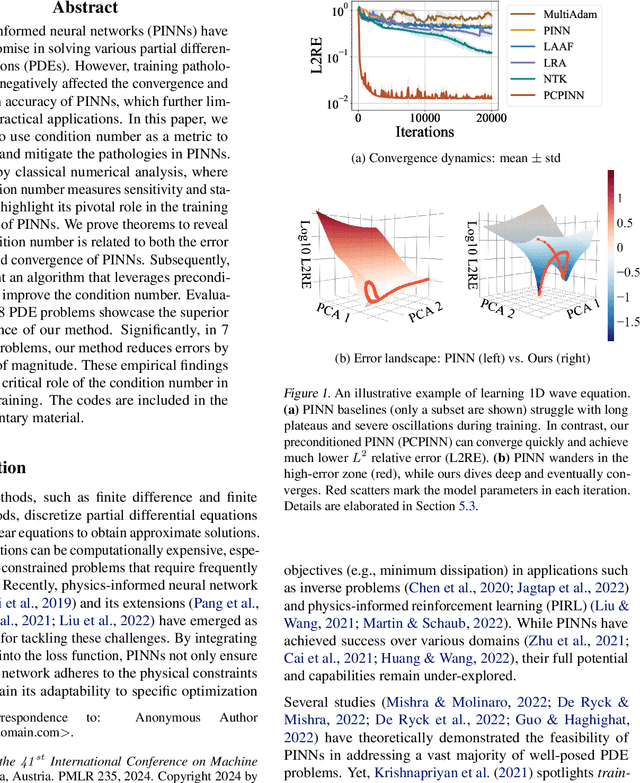
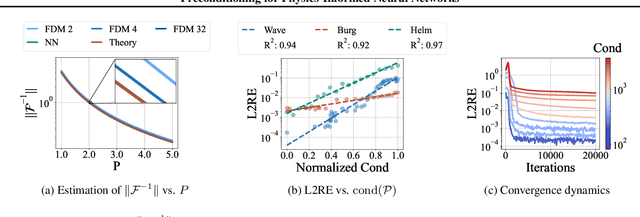
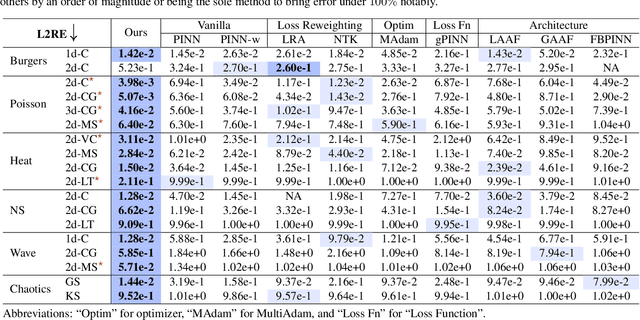
Physics-informed neural networks (PINNs) have shown promise in solving various partial differential equations (PDEs). However, training pathologies have negatively affected the convergence and prediction accuracy of PINNs, which further limits their practical applications. In this paper, we propose to use condition number as a metric to diagnose and mitigate the pathologies in PINNs. Inspired by classical numerical analysis, where the condition number measures sensitivity and stability, we highlight its pivotal role in the training dynamics of PINNs. We prove theorems to reveal how condition number is related to both the error control and convergence of PINNs. Subsequently, we present an algorithm that leverages preconditioning to improve the condition number. Evaluations of 18 PDE problems showcase the superior performance of our method. Significantly, in 7 of these problems, our method reduces errors by an order of magnitude. These empirical findings verify the critical role of the condition number in PINNs' training.

Learning to Segment from Noisy Annotations: A Spatial Correction Approach

Noisy labels can significantly affect the performance of deep neural networks (DNNs). In medical image segmentation tasks, annotations are error-prone due to the high demand in annotation time and in the annotators' expertise. Existing methods mostly assume noisy labels in different pixels are \textit{i.i.d}. However, segmentation label noise usually has strong spatial correlation and has prominent bias in distribution. In this paper, we propose a novel Markov model for segmentation noisy annotations that encodes both spatial correlation and bias. Further, to mitigate such label noise, we propose a label correction method to recover true label progressively. We provide theoretical guarantees of the correctness of the proposed method. Experiments show that our approach outperforms current state-of-the-art methods on both synthetic and real-world noisy annotations.

PINNacle: A Comprehensive Benchmark of Physics-Informed Neural Networks for Solving PDEs

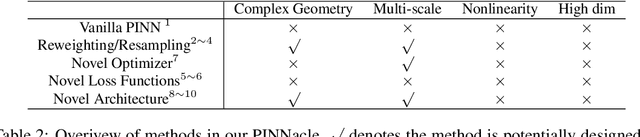
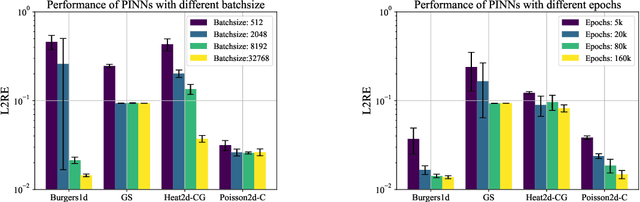
While significant progress has been made on Physics-Informed Neural Networks (PINNs), a comprehensive comparison of these methods across a wide range of Partial Differential Equations (PDEs) is still lacking. This study introduces PINNacle, a benchmarking tool designed to fill this gap. PINNacle provides a diverse dataset, comprising over 20 distinct PDEs from various domains including heat conduction, fluid dynamics, biology, and electromagnetics. These PDEs encapsulate key challenges inherent to real-world problems, such as complex geometry, multi-scale phenomena, nonlinearity, and high dimensionality. PINNacle also offers a user-friendly toolbox, incorporating about 10 state-of-the-art PINN methods for systematic evaluation and comparison. We have conducted extensive experiments with these methods, offering insights into their strengths and weaknesses. In addition to providing a standardized means of assessing performance, PINNacle also offers an in-depth analysis to guide future research, particularly in areas such as domain decomposition methods and loss reweighting for handling multi-scale problems and complex geometry. While PINNacle does not guarantee success in all real-world scenarios, it represents a significant contribution to the field by offering a robust, diverse, and comprehensive benchmark suite that will undoubtedly foster further research and development in PINNs.

MultiAdam: Parameter-wise Scale-invariant Optimizer for Multiscale Training of Physics-informed Neural Networks

Physics-informed Neural Networks (PINNs) have recently achieved remarkable progress in solving Partial Differential Equations (PDEs) in various fields by minimizing a weighted sum of PDE loss and boundary loss. However, there are several critical challenges in the training of PINNs, including the lack of theoretical frameworks and the imbalance between PDE loss and boundary loss. In this paper, we present an analysis of second-order non-homogeneous PDEs, which are classified into three categories and applicable to various common problems. We also characterize the connections between the training loss and actual error, guaranteeing convergence under mild conditions. The theoretical analysis inspires us to further propose MultiAdam, a scale-invariant optimizer that leverages gradient momentum to parameter-wisely balance the loss terms. Extensive experiment results on multiple problems from different physical domains demonstrate that our MultiAdam solver can improve the predictive accuracy by 1-2 orders of magnitude compared with strong baselines.