Songming Liu
RDT2: Exploring the Scaling Limit of UMI Data Towards Zero-Shot Cross-Embodiment Generalization
Feb 03, 2026Abstract:Vision-Language-Action (VLA) models hold promise for generalist robotics but currently struggle with data scarcity, architectural inefficiencies, and the inability to generalize across different hardware platforms. We introduce RDT2, a robotic foundation model built upon a 7B parameter VLM designed to enable zero-shot deployment on novel embodiments for open-vocabulary tasks. To achieve this, we collected one of the largest open-source robotic datasets--over 10,000 hours of demonstrations in diverse families--using an enhanced, embodiment-agnostic Universal Manipulation Interface (UMI). Our approach employs a novel three-stage training recipe that aligns discrete linguistic knowledge with continuous control via Residual Vector Quantization (RVQ), flow-matching, and distillation for real-time inference. Consequently, RDT2 becomes one of the first models that simultaneously zero-shot generalizes to unseen objects, scenes, instructions, and even robotic platforms. Besides, it outperforms state-of-the-art baselines in dexterous, long-horizon, and dynamic downstream tasks like playing table tennis. See https://rdt-robotics.github.io/rdt2/ for more information.
From reactive to cognitive: brain-inspired spatial intelligence for embodied agents
Aug 24, 2025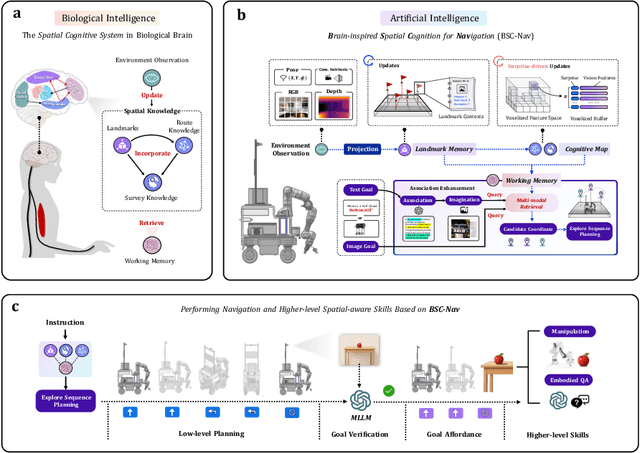
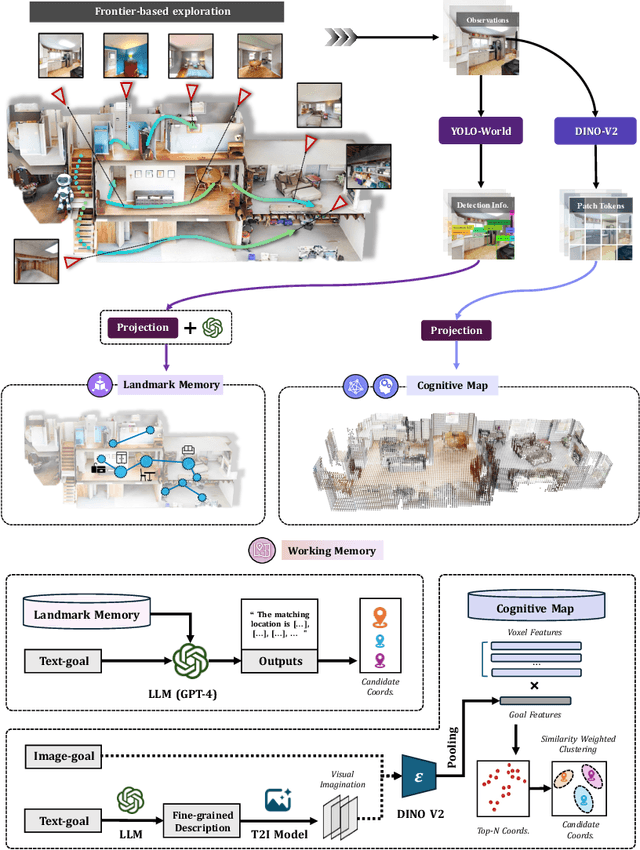
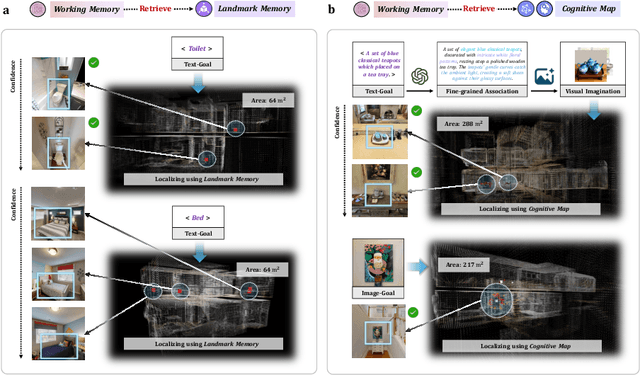
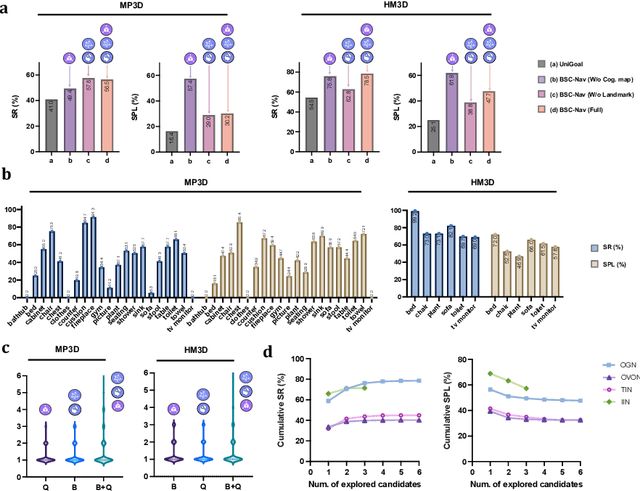
Abstract:Spatial cognition enables adaptive goal-directed behavior by constructing internal models of space. Robust biological systems consolidate spatial knowledge into three interconnected forms: \textit{landmarks} for salient cues, \textit{route knowledge} for movement trajectories, and \textit{survey knowledge} for map-like representations. While recent advances in multi-modal large language models (MLLMs) have enabled visual-language reasoning in embodied agents, these efforts lack structured spatial memory and instead operate reactively, limiting their generalization and adaptability in complex real-world environments. Here we present Brain-inspired Spatial Cognition for Navigation (BSC-Nav), a unified framework for constructing and leveraging structured spatial memory in embodied agents. BSC-Nav builds allocentric cognitive maps from egocentric trajectories and contextual cues, and dynamically retrieves spatial knowledge aligned with semantic goals. Integrated with powerful MLLMs, BSC-Nav achieves state-of-the-art efficacy and efficiency across diverse navigation tasks, demonstrates strong zero-shot generalization, and supports versatile embodied behaviors in the real physical world, offering a scalable and biologically grounded path toward general-purpose spatial intelligence.
ManiBox: Enhancing Spatial Grasping Generalization via Scalable Simulation Data Generation
Nov 04, 2024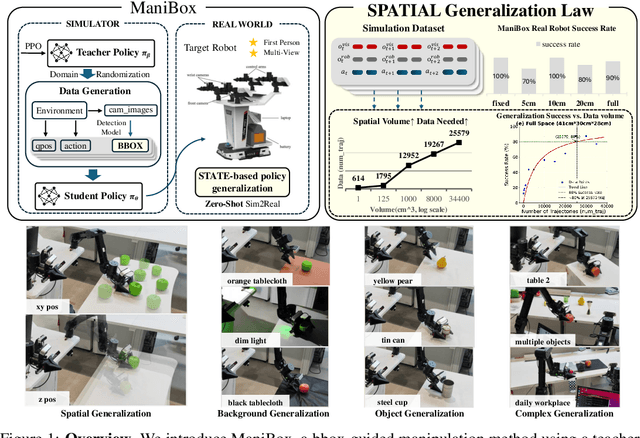

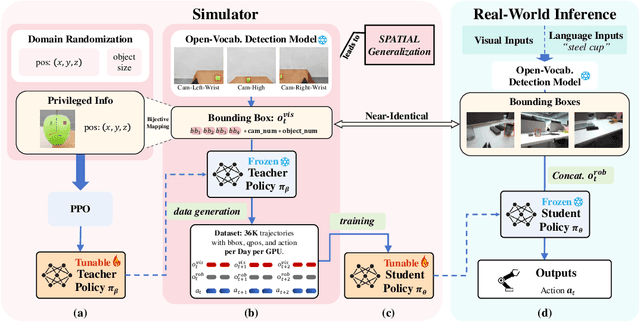

Abstract:Learning a precise robotic grasping policy is crucial for embodied agents operating in complex real-world manipulation tasks. Despite significant advancements, most models still struggle with accurate spatial positioning of objects to be grasped. We first show that this spatial generalization challenge stems primarily from the extensive data requirements for adequate spatial understanding. However, collecting such data with real robots is prohibitively expensive, and relying on simulation data often leads to visual generalization gaps upon deployment. To overcome these challenges, we then focus on state-based policy generalization and present \textbf{ManiBox}, a novel bounding-box-guided manipulation method built on a simulation-based teacher-student framework. The teacher policy efficiently generates scalable simulation data using bounding boxes, which are proven to uniquely determine the objects' spatial positions. The student policy then utilizes these low-dimensional spatial states to enable zero-shot transfer to real robots. Through comprehensive evaluations in simulated and real-world environments, ManiBox demonstrates a marked improvement in spatial grasping generalization and adaptability to diverse objects and backgrounds. Further, our empirical study into scaling laws for policy performance indicates that spatial volume generalization scales positively with data volume. For a certain level of spatial volume, the success rate of grasping empirically follows Michaelis-Menten kinetics relative to data volume, showing a saturation effect as data increases. Our videos and code are available in https://thkkk.github.io/manibox.
RDT-1B: a Diffusion Foundation Model for Bimanual Manipulation
Oct 10, 2024



Abstract:Bimanual manipulation is essential in robotics, yet developing foundation models is extremely challenging due to the inherent complexity of coordinating two robot arms (leading to multi-modal action distributions) and the scarcity of training data. In this paper, we present the Robotics Diffusion Transformer (RDT), a pioneering diffusion foundation model for bimanual manipulation. RDT builds on diffusion models to effectively represent multi-modality, with innovative designs of a scalable Transformer to deal with the heterogeneity of multi-modal inputs and to capture the nonlinearity and high frequency of robotic data. To address data scarcity, we further introduce a Physically Interpretable Unified Action Space, which can unify the action representations of various robots while preserving the physical meanings of original actions, facilitating learning transferrable physical knowledge. With these designs, we managed to pre-train RDT on the largest collection of multi-robot datasets to date and scaled it up to 1.2B parameters, which is the largest diffusion-based foundation model for robotic manipulation. We finally fine-tuned RDT on a self-created multi-task bimanual dataset with over 6K+ episodes to refine its manipulation capabilities. Experiments on real robots demonstrate that RDT significantly outperforms existing methods. It exhibits zero-shot generalization to unseen objects and scenes, understands and follows language instructions, learns new skills with just 1~5 demonstrations, and effectively handles complex, dexterous tasks. We refer to https://rdt-robotics.github.io/rdt-robotics/ for the code and videos.
Fourier Controller Networks for Real-Time Decision-Making in Embodied Learning
May 30, 2024Abstract:Reinforcement learning is able to obtain generalized low-level robot policies on diverse robotics datasets in embodied learning scenarios, and Transformer has been widely used to model time-varying features. However, it still suffers from the issues of low data efficiency and high inference latency. In this paper, we propose to investigate the task from a new perspective of the frequency domain. We first observe that the energy density in the frequency domain of a robot's trajectory is mainly concentrated in the low-frequency part. Then, we present the Fourier Controller Network (FCNet), a new network that utilizes the Short-Time Fourier Transform (STFT) to extract and encode time-varying features through frequency domain interpolation. We further achieve parallel training and efficient recurrent inference by using FFT and Sliding DFT methods in the model architecture for real-time decision-making. Comprehensive analyses in both simulated (e.g., D4RL) and real-world environments (e.g., robot locomotion) demonstrate FCNet's substantial efficiency and effectiveness over existing methods such as Transformer, e.g., FCNet outperforms Transformer on multi-environmental robotics datasets of all types of sizes (from 1.9M to 120M). The project page and code can be found https://thkkk.github.io/fcnet.
Reference Neural Operators: Learning the Smooth Dependence of Solutions of PDEs on Geometric Deformations
May 27, 2024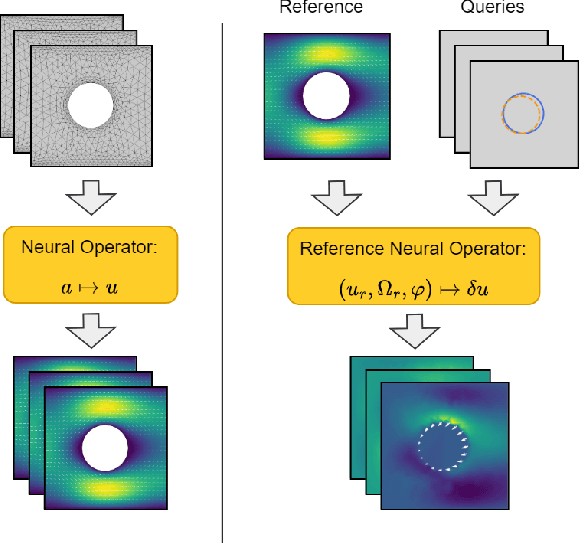
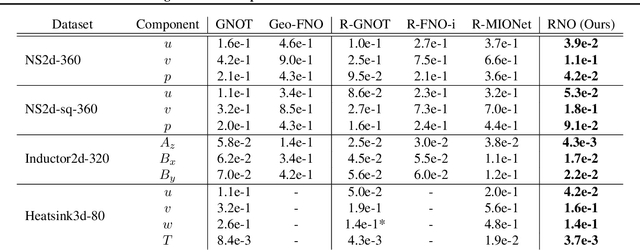
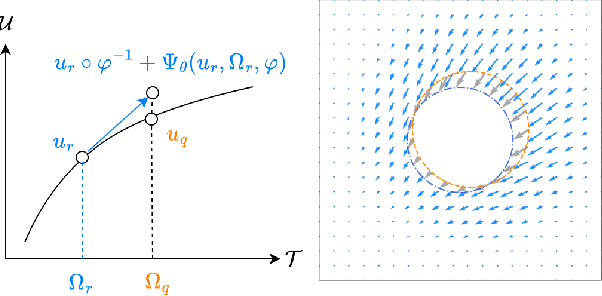

Abstract:For partial differential equations on domains of arbitrary shapes, existing works of neural operators attempt to learn a mapping from geometries to solutions. It often requires a large dataset of geometry-solution pairs in order to obtain a sufficiently accurate neural operator. However, for many industrial applications, e.g., engineering design optimization, it can be prohibitive to satisfy the requirement since even a single simulation may take hours or days of computation. To address this issue, we propose reference neural operators (RNO), a novel way of implementing neural operators, i.e., to learn the smooth dependence of solutions on geometric deformations. Specifically, given a reference solution, RNO can predict solutions corresponding to arbitrary deformations of the referred geometry. This approach turns out to be much more data efficient. Through extensive experiments, we show that RNO can learn the dependence across various types and different numbers of geometry objects with relatively small datasets. RNO outperforms baseline models in accuracy by a large lead and achieves up to 80% error reduction.
DPOT: Auto-Regressive Denoising Operator Transformer for Large-Scale PDE Pre-Training
Mar 08, 2024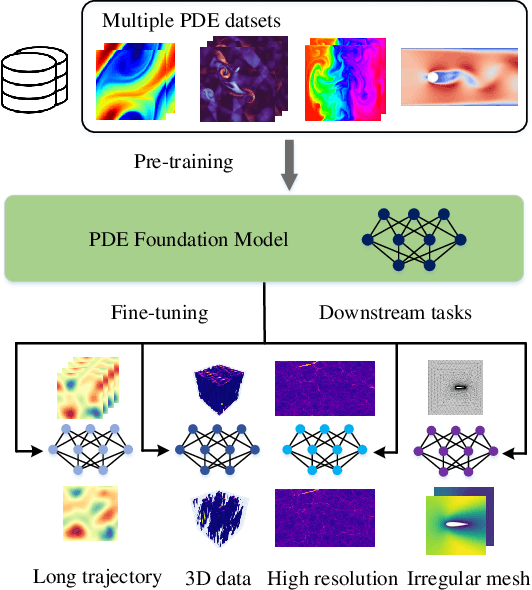
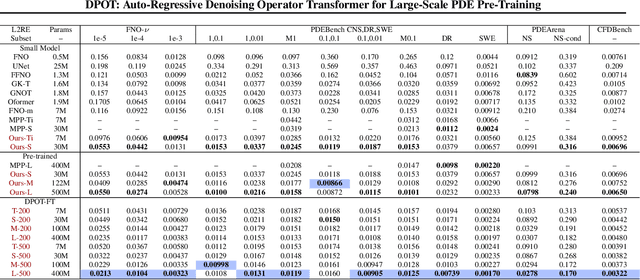
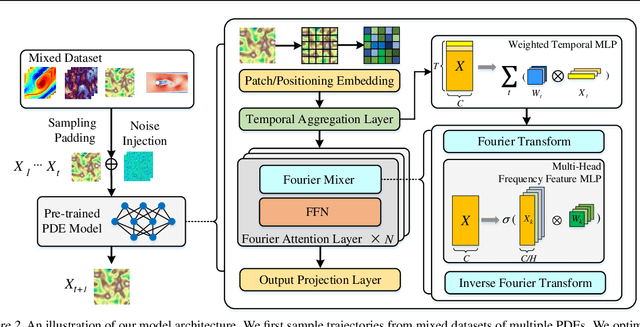
Abstract:Pre-training has been investigated to improve the efficiency and performance of training neural operators in data-scarce settings. However, it is largely in its infancy due to the inherent complexity and diversity, such as long trajectories, multiple scales and varying dimensions of partial differential equations (PDEs) data. In this paper, we present a new auto-regressive denoising pre-training strategy, which allows for more stable and efficient pre-training on PDE data and generalizes to various downstream tasks. Moreover, by designing a flexible and scalable model architecture based on Fourier attention, we can easily scale up the model for large-scale pre-training. We train our PDE foundation model with up to 0.5B parameters on 10+ PDE datasets with more than 100k trajectories. Extensive experiments show that we achieve SOTA on these benchmarks and validate the strong generalizability of our model to significantly enhance performance on diverse downstream PDE tasks like 3D data. Code is available at \url{https://github.com/thu-ml/DPOT}.
Preconditioning for Physics-Informed Neural Networks
Feb 01, 2024

Abstract:Physics-informed neural networks (PINNs) have shown promise in solving various partial differential equations (PDEs). However, training pathologies have negatively affected the convergence and prediction accuracy of PINNs, which further limits their practical applications. In this paper, we propose to use condition number as a metric to diagnose and mitigate the pathologies in PINNs. Inspired by classical numerical analysis, where the condition number measures sensitivity and stability, we highlight its pivotal role in the training dynamics of PINNs. We prove theorems to reveal how condition number is related to both the error control and convergence of PINNs. Subsequently, we present an algorithm that leverages preconditioning to improve the condition number. Evaluations of 18 PDE problems showcase the superior performance of our method. Significantly, in 7 of these problems, our method reduces errors by an order of magnitude. These empirical findings verify the critical role of the condition number in PINNs' training.
PINNacle: A Comprehensive Benchmark of Physics-Informed Neural Networks for Solving PDEs
Jun 15, 2023

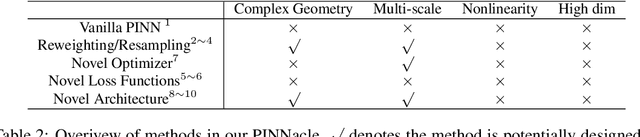
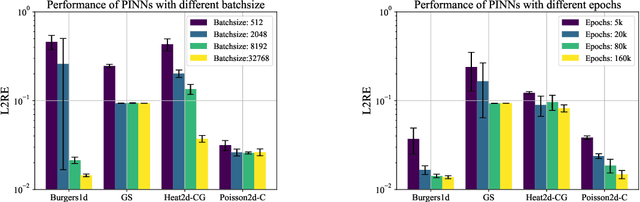
Abstract:While significant progress has been made on Physics-Informed Neural Networks (PINNs), a comprehensive comparison of these methods across a wide range of Partial Differential Equations (PDEs) is still lacking. This study introduces PINNacle, a benchmarking tool designed to fill this gap. PINNacle provides a diverse dataset, comprising over 20 distinct PDEs from various domains including heat conduction, fluid dynamics, biology, and electromagnetics. These PDEs encapsulate key challenges inherent to real-world problems, such as complex geometry, multi-scale phenomena, nonlinearity, and high dimensionality. PINNacle also offers a user-friendly toolbox, incorporating about 10 state-of-the-art PINN methods for systematic evaluation and comparison. We have conducted extensive experiments with these methods, offering insights into their strengths and weaknesses. In addition to providing a standardized means of assessing performance, PINNacle also offers an in-depth analysis to guide future research, particularly in areas such as domain decomposition methods and loss reweighting for handling multi-scale problems and complex geometry. While PINNacle does not guarantee success in all real-world scenarios, it represents a significant contribution to the field by offering a robust, diverse, and comprehensive benchmark suite that will undoubtedly foster further research and development in PINNs.
MultiAdam: Parameter-wise Scale-invariant Optimizer for Multiscale Training of Physics-informed Neural Networks
Jun 05, 2023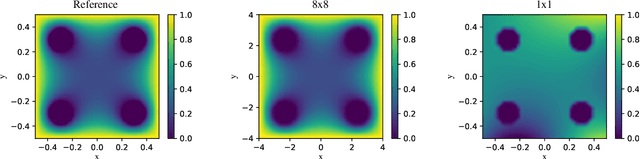
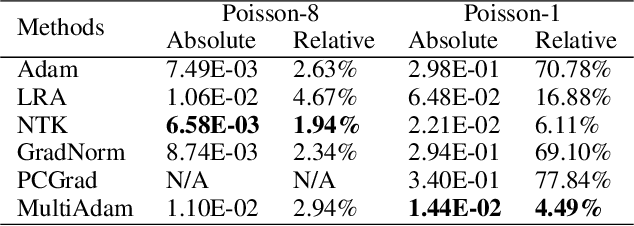
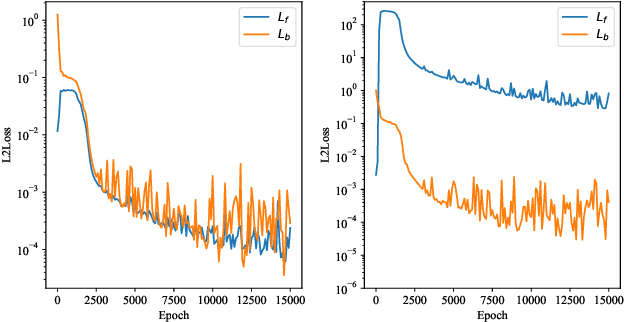
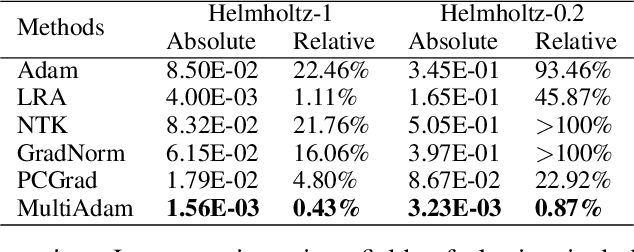
Abstract:Physics-informed Neural Networks (PINNs) have recently achieved remarkable progress in solving Partial Differential Equations (PDEs) in various fields by minimizing a weighted sum of PDE loss and boundary loss. However, there are several critical challenges in the training of PINNs, including the lack of theoretical frameworks and the imbalance between PDE loss and boundary loss. In this paper, we present an analysis of second-order non-homogeneous PDEs, which are classified into three categories and applicable to various common problems. We also characterize the connections between the training loss and actual error, guaranteeing convergence under mild conditions. The theoretical analysis inspires us to further propose MultiAdam, a scale-invariant optimizer that leverages gradient momentum to parameter-wisely balance the loss terms. Extensive experiment results on multiple problems from different physical domains demonstrate that our MultiAdam solver can improve the predictive accuracy by 1-2 orders of magnitude compared with strong baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge