Operator Learning with Domain Decomposition for Geometry Generalization in PDE Solving

Neural operators have become increasingly popular in solving \textit{partial differential equations} (PDEs) due to their superior capability to capture intricate mappings between function spaces over complex domains. However, the data-hungry nature of operator learning inevitably poses a bottleneck for their widespread applications. At the core of the challenge lies the absence of transferability of neural operators to new geometries. To tackle this issue, we propose operator learning with domain decomposition, a local-to-global framework to solve PDEs on arbitrary geometries. Under this framework, we devise an iterative scheme \textit{Schwarz Neural Inference} (SNI). This scheme allows for partitioning of the problem domain into smaller subdomains, on which local problems can be solved with neural operators, and stitching local solutions to construct a global solution. Additionally, we provide a theoretical analysis of the convergence rate and error bound. We conduct extensive experiments on several representative PDEs with diverse boundary conditions and achieve remarkable geometry generalization compared to alternative methods. These analysis and experiments demonstrate the proposed framework's potential in addressing challenges related to geometry generalization and data efficiency.

Reference Neural Operators: Learning the Smooth Dependence of Solutions of PDEs on Geometric Deformations

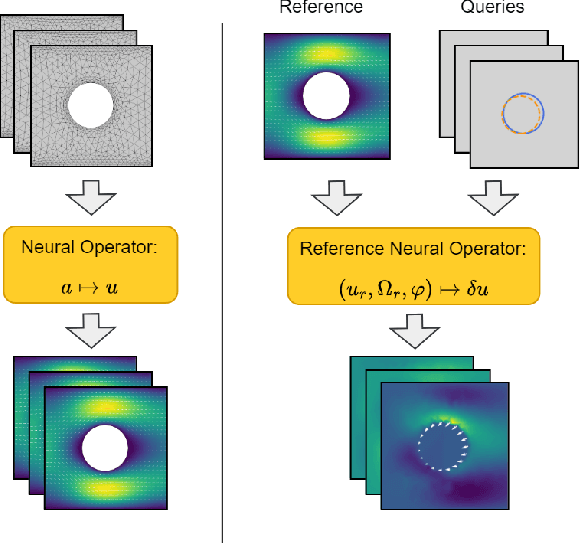
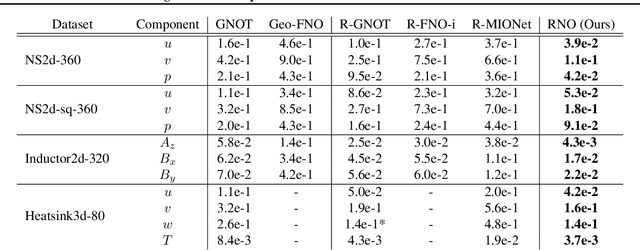
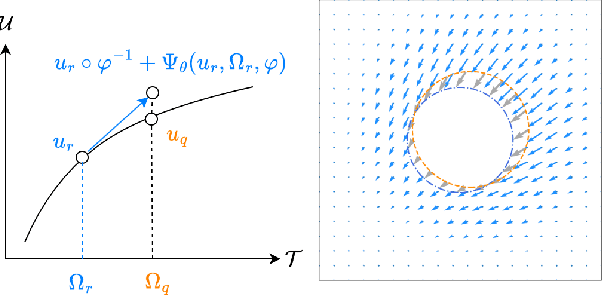
For partial differential equations on domains of arbitrary shapes, existing works of neural operators attempt to learn a mapping from geometries to solutions. It often requires a large dataset of geometry-solution pairs in order to obtain a sufficiently accurate neural operator. However, for many industrial applications, e.g., engineering design optimization, it can be prohibitive to satisfy the requirement since even a single simulation may take hours or days of computation. To address this issue, we propose reference neural operators (RNO), a novel way of implementing neural operators, i.e., to learn the smooth dependence of solutions on geometric deformations. Specifically, given a reference solution, RNO can predict solutions corresponding to arbitrary deformations of the referred geometry. This approach turns out to be much more data efficient. Through extensive experiments, we show that RNO can learn the dependence across various types and different numbers of geometry objects with relatively small datasets. RNO outperforms baseline models in accuracy by a large lead and achieves up to 80% error reduction.

Preconditioning for Physics-Informed Neural Networks

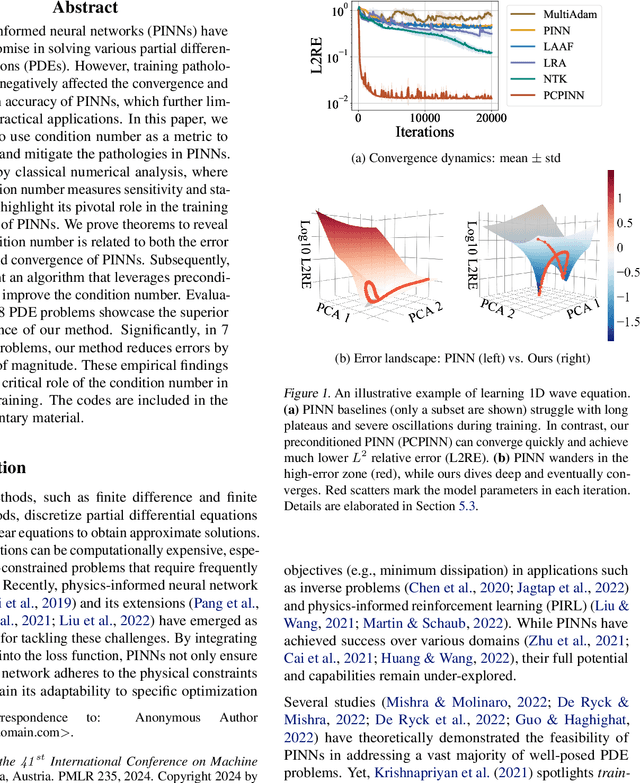
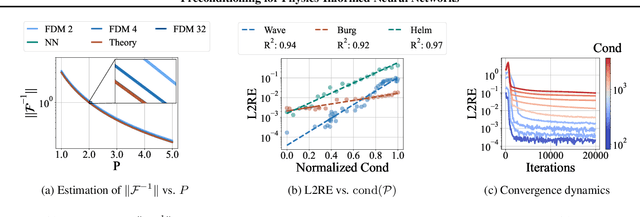
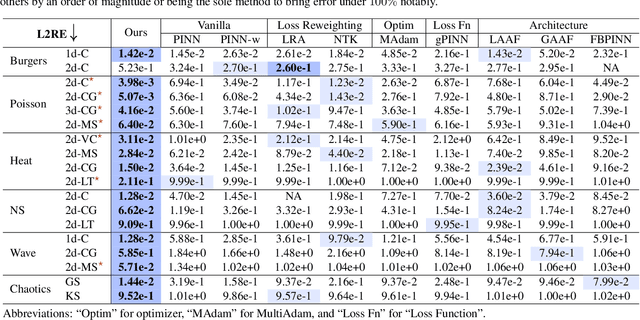
Physics-informed neural networks (PINNs) have shown promise in solving various partial differential equations (PDEs). However, training pathologies have negatively affected the convergence and prediction accuracy of PINNs, which further limits their practical applications. In this paper, we propose to use condition number as a metric to diagnose and mitigate the pathologies in PINNs. Inspired by classical numerical analysis, where the condition number measures sensitivity and stability, we highlight its pivotal role in the training dynamics of PINNs. We prove theorems to reveal how condition number is related to both the error control and convergence of PINNs. Subsequently, we present an algorithm that leverages preconditioning to improve the condition number. Evaluations of 18 PDE problems showcase the superior performance of our method. Significantly, in 7 of these problems, our method reduces errors by an order of magnitude. These empirical findings verify the critical role of the condition number in PINNs' training.