A$^2$Search: Ambiguity-Aware Question Answering with Reinforcement Learning

Recent advances in Large Language Models (LLMs) and Reinforcement Learning (RL) have led to strong performance in open-domain question answering (QA). However, existing models still struggle with questions that admit multiple valid answers. Standard QA benchmarks, which typically assume a single gold answer, overlook this reality and thus produce inappropriate training signals. Existing attempts to handle ambiguity often rely on costly manual annotation, which is difficult to scale to multi-hop datasets such as HotpotQA and MuSiQue. In this paper, we present A$^2$Search, an annotation-free, end-to-end training framework to recognize and handle ambiguity. At its core is an automated pipeline that detects ambiguous questions and gathers alternative answers via trajectory sampling and evidence verification. The model is then optimized with RL using a carefully designed $\mathrm{AnsF1}$ reward, which naturally accommodates multiple answers. Experiments on eight open-domain QA benchmarks demonstrate that A$^2$Search achieves new state-of-the-art performance. With only a single rollout, A$^2$Search-7B yields an average $\mathrm{AnsF1}@1$ score of $48.4\%$ across four multi-hop benchmarks, outperforming all strong baselines, including the substantially larger ReSearch-32B ($46.2\%$). Extensive analyses further show that A$^2$Search resolves ambiguity and generalizes across benchmarks, highlighting that embracing ambiguity is essential for building more reliable QA systems. Our code, data, and model weights can be found at https://github.com/zfj1998/A2Search

Accelerating PDE-Constrained Optimization by the Derivative of Neural Operators

PDE-Constrained Optimization (PDECO) problems can be accelerated significantly by employing gradient-based methods with surrogate models like neural operators compared to traditional numerical solvers. However, this approach faces two key challenges: (1) **Data inefficiency**: Lack of efficient data sampling and effective training for neural operators, particularly for optimization purpose. (2) **Instability**: High risk of optimization derailment due to inaccurate neural operator predictions and gradients. To address these challenges, we propose a novel framework: (1) **Optimization-oriented training**: we leverage data from full steps of traditional optimization algorithms and employ a specialized training method for neural operators. (2) **Enhanced derivative learning**: We introduce a *Virtual-Fourier* layer to enhance derivative learning within the neural operator, a crucial aspect for gradient-based optimization. (3) **Hybrid optimization**: We implement a hybrid approach that integrates neural operators with numerical solvers, providing robust regularization for the optimization process. Our extensive experimental results demonstrate the effectiveness of our model in accurately learning operators and their derivatives. Furthermore, our hybrid optimization approach exhibits robust convergence.

Exploratory Diffusion Policy for Unsupervised Reinforcement Learning

Unsupervised reinforcement learning (RL) aims to pre-train agents by exploring states or skills in reward-free environments, facilitating the adaptation to downstream tasks. However, existing methods often overlook the fitting ability of pre-trained policies and struggle to handle the heterogeneous pre-training data, which are crucial for achieving efficient exploration and fast fine-tuning. To address this gap, we propose Exploratory Diffusion Policy (EDP), which leverages the strong expressive ability of diffusion models to fit the explored data, both boosting exploration and obtaining an efficient initialization for downstream tasks. Specifically, we estimate the distribution of collected data in the replay buffer with the diffusion policy and propose a score intrinsic reward, encouraging the agent to explore unseen states. For fine-tuning the pre-trained diffusion policy on downstream tasks, we provide both theoretical analyses and practical algorithms, including an alternating method of Q function optimization and diffusion policy distillation. Extensive experiments demonstrate the effectiveness of EDP in efficient exploration during pre-training and fast adaptation during fine-tuning.

PAPM: A Physics-aware Proxy Model for Process Systems

In the context of proxy modeling for process systems, traditional data-driven deep learning approaches frequently encounter significant challenges, such as substantial training costs induced by large amounts of data, and limited generalization capabilities. As a promising alternative, physics-aware models incorporate partial physics knowledge to ameliorate these challenges. Although demonstrating efficacy, they fall short in terms of exploration depth and universality. To address these shortcomings, we introduce a physics-aware proxy model (PAPM) that fully incorporates partial prior physics of process systems, which includes multiple input conditions and the general form of conservation relations, resulting in better out-of-sample generalization. Additionally, PAPM contains a holistic temporal-spatial stepping module for flexible adaptation across various process systems. Through systematic comparisons with state-of-the-art pure data-driven and physics-aware models across five two-dimensional benchmarks in nine generalization tasks, PAPM notably achieves an average performance improvement of 6.7%, while requiring fewer FLOPs, and just 1% of the parameters compared to the prior leading method. The code is available at https://github.com/pengwei07/PAPM.

Reference Neural Operators: Learning the Smooth Dependence of Solutions of PDEs on Geometric Deformations

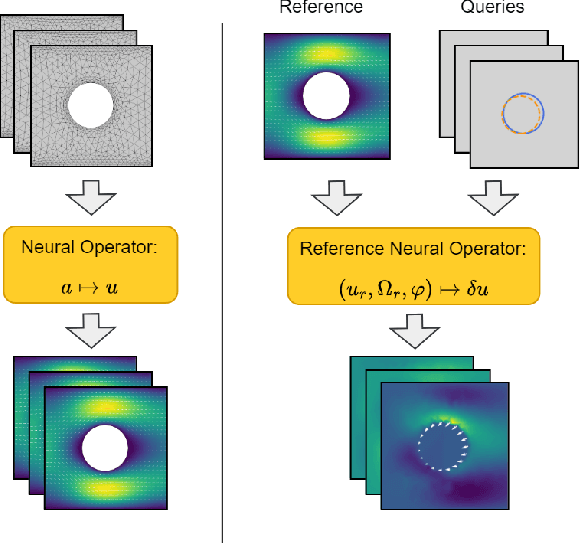
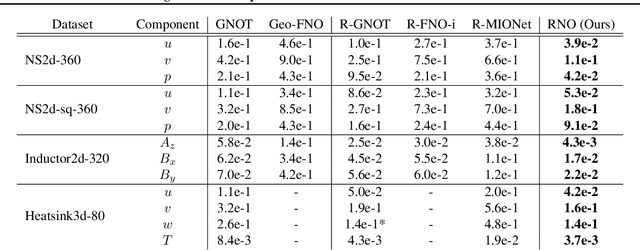
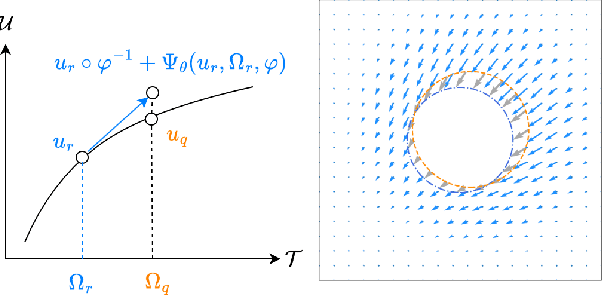
For partial differential equations on domains of arbitrary shapes, existing works of neural operators attempt to learn a mapping from geometries to solutions. It often requires a large dataset of geometry-solution pairs in order to obtain a sufficiently accurate neural operator. However, for many industrial applications, e.g., engineering design optimization, it can be prohibitive to satisfy the requirement since even a single simulation may take hours or days of computation. To address this issue, we propose reference neural operators (RNO), a novel way of implementing neural operators, i.e., to learn the smooth dependence of solutions on geometric deformations. Specifically, given a reference solution, RNO can predict solutions corresponding to arbitrary deformations of the referred geometry. This approach turns out to be much more data efficient. Through extensive experiments, we show that RNO can learn the dependence across various types and different numbers of geometry objects with relatively small datasets. RNO outperforms baseline models in accuracy by a large lead and achieves up to 80% error reduction.

PEAC: Unsupervised Pre-training for Cross-Embodiment Reinforcement Learning

Designing generalizable agents capable of adapting to diverse embodiments has achieved significant attention in Reinforcement Learning (RL), which is critical for deploying RL agents in various real-world applications. Previous Cross-Embodiment RL approaches have focused on transferring knowledge across embodiments within specific tasks. These methods often result in knowledge tightly coupled with those tasks and fail to adequately capture the distinct characteristics of different embodiments. To address this limitation, we introduce the notion of Cross-Embodiment Unsupervised RL (CEURL), which leverages unsupervised learning to enable agents to acquire embodiment-aware and task-agnostic knowledge through online interactions within reward-free environments. We formulate CEURL as a novel Controlled Embodiment Markov Decision Process (CE-MDP) and systematically analyze CEURL's pre-training objectives under CE-MDP. Based on these analyses, we develop a novel algorithm Pre-trained Embodiment-Aware Control (PEAC) for handling CEURL, incorporating an intrinsic reward function specifically designed for cross-embodiment pre-training. PEAC not only provides an intuitive optimization strategy for cross-embodiment pre-training but also can integrate flexibly with existing unsupervised RL methods, facilitating cross-embodiment exploration and skill discovery. Extensive experiments in both simulated (e.g., DMC and Robosuite) and real-world environments (e.g., legged locomotion) demonstrate that PEAC significantly improves adaptation performance and cross-embodiment generalization, demonstrating its effectiveness in overcoming the unique challenges of CEURL.

DPOT: Auto-Regressive Denoising Operator Transformer for Large-Scale PDE Pre-Training

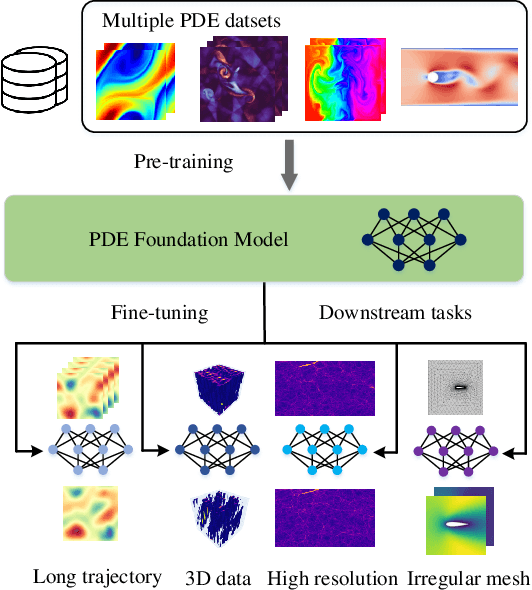
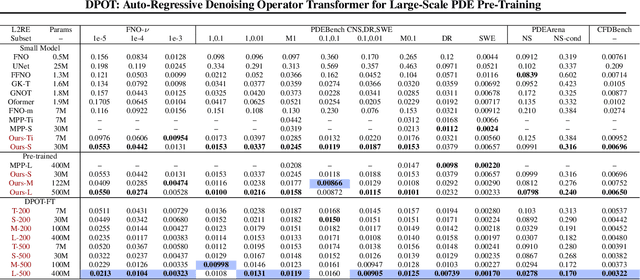
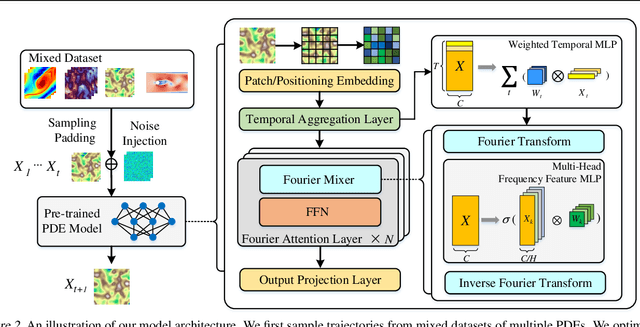
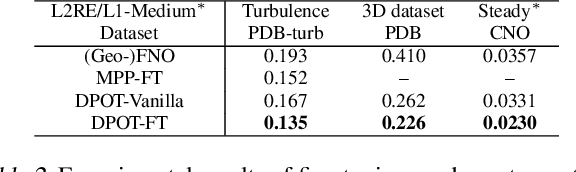
Pre-training has been investigated to improve the efficiency and performance of training neural operators in data-scarce settings. However, it is largely in its infancy due to the inherent complexity and diversity, such as long trajectories, multiple scales and varying dimensions of partial differential equations (PDEs) data. In this paper, we present a new auto-regressive denoising pre-training strategy, which allows for more stable and efficient pre-training on PDE data and generalizes to various downstream tasks. Moreover, by designing a flexible and scalable model architecture based on Fourier attention, we can easily scale up the model for large-scale pre-training. We train our PDE foundation model with up to 0.5B parameters on 10+ PDE datasets with more than 100k trajectories. Extensive experiments show that we achieve SOTA on these benchmarks and validate the strong generalizability of our model to significantly enhance performance on diverse downstream PDE tasks like 3D data. Code is available at \url{https://github.com/thu-ml/DPOT}.

Your Diffusion Model is Secretly a Certifiably Robust Classifier

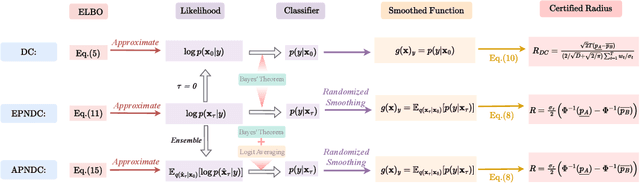
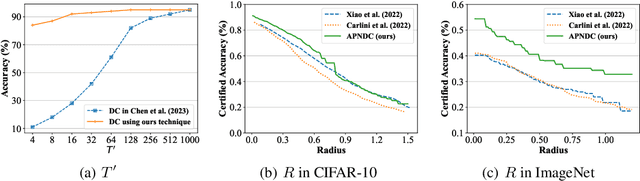
Diffusion models are recently employed as generative classifiers for robust classification. However, a comprehensive theoretical understanding of the robustness of diffusion classifiers is still lacking, leading us to question whether they will be vulnerable to future stronger attacks. In this study, we propose a new family of diffusion classifiers, named Noised Diffusion Classifiers~(NDCs), that possess state-of-the-art certified robustness. Specifically, we generalize the diffusion classifiers to classify Gaussian-corrupted data by deriving the evidence lower bounds (ELBOs) for these distributions, approximating the likelihood using the ELBO, and calculating classification probabilities via Bayes' theorem. We integrate these generalized diffusion classifiers with randomized smoothing to construct smoothed classifiers possessing non-constant Lipschitzness. Experimental results demonstrate the superior certified robustness of our proposed NDCs. Notably, we are the first to achieve 80\%+ and 70\%+ certified robustness on CIFAR-10 under adversarial perturbations with $\ell_2$ norm less than 0.25 and 0.5, respectively, using a single off-the-shelf diffusion model without any additional data.

Preconditioning for Physics-Informed Neural Networks

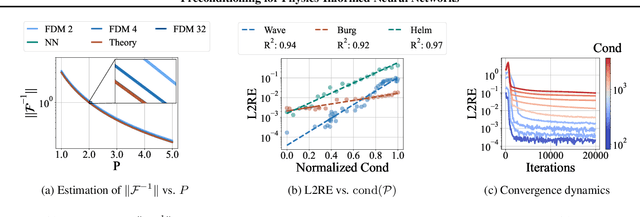
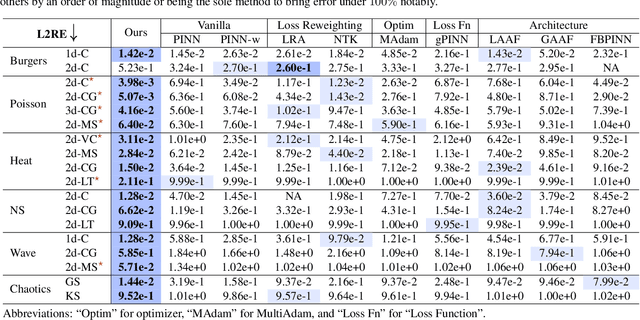
Physics-informed neural networks (PINNs) have shown promise in solving various partial differential equations (PDEs). However, training pathologies have negatively affected the convergence and prediction accuracy of PINNs, which further limits their practical applications. In this paper, we propose to use condition number as a metric to diagnose and mitigate the pathologies in PINNs. Inspired by classical numerical analysis, where the condition number measures sensitivity and stability, we highlight its pivotal role in the training dynamics of PINNs. We prove theorems to reveal how condition number is related to both the error control and convergence of PINNs. Subsequently, we present an algorithm that leverages preconditioning to improve the condition number. Evaluations of 18 PDE problems showcase the superior performance of our method. Significantly, in 7 of these problems, our method reduces errors by an order of magnitude. These empirical findings verify the critical role of the condition number in PINNs' training.

Accelerating Data Generation for Neural Operators via Krylov Subspace Recycling

Learning neural operators for solving partial differential equations (PDEs) has attracted great attention due to its high inference efficiency. However, training such operators requires generating a substantial amount of labeled data, i.e., PDE problems together with their solutions. The data generation process is exceptionally time-consuming, as it involves solving numerous systems of linear equations to obtain numerical solutions to the PDEs. Many existing methods solve these systems independently without considering their inherent similarities, resulting in extremely redundant computations. To tackle this problem, we propose a novel method, namely Sorting Krylov Recycling (SKR), to boost the efficiency of solving these systems, thus significantly accelerating data generation for neural operators training. To the best of our knowledge, SKR is the first attempt to address the time-consuming nature of data generation for learning neural operators. The working horse of SKR is Krylov subspace recycling, a powerful technique for solving a series of interrelated systems by leveraging their inherent similarities. Specifically, SKR employs a sorting algorithm to arrange these systems in a sequence, where adjacent systems exhibit high similarities. Then it equips a solver with Krylov subspace recycling to solve the systems sequentially instead of independently, thus effectively enhancing the solving efficiency. Both theoretical analysis and extensive experiments demonstrate that SKR can significantly accelerate neural operator data generation, achieving a remarkable speedup of up to 13.9 times.