MatryoshkaKV: Adaptive KV Compression via Trainable Orthogonal Projection

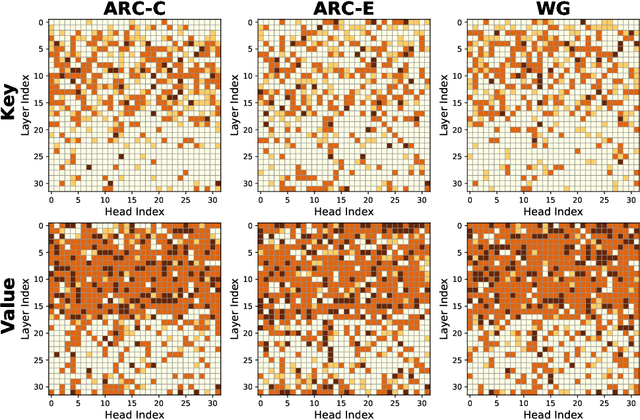
KV cache has become a de facto technique for the inference of large language models (LLMs), where tensors of shape (layer number, head number, sequence length, feature dimension) are introduced to cache historical information for self-attention. As the size of the model and data grows, the KV cache can quickly become a bottleneck within the system in both storage and memory transfer. To address this, prior studies usually focus on the first three axes of the cache tensors for compression. This paper supplements them, focusing on the feature dimension axis, by utilizing low-rank projection matrices to transform the cache features into spaces with reduced dimensions. We begin by investigating the canonical orthogonal projection method for data compression through principal component analysis (PCA). We observe the issue with PCA projection where significant performance degradation is observed at low compression rates. To bridge the gap, we propose to directly tune the orthogonal projection matrices with a distillation objective using an elaborate Matryoshka training strategy. After training, we adaptively search for the optimal compression rates for various layers and heads given varying compression budgets. Compared to previous works, our method can easily embrace pre-trained LLMs and hold a smooth tradeoff between performance and compression rate. We empirically witness the high data efficiency of our training procedure and find that our method can sustain over 90% performance with an average KV cache compression rate of 60% (and up to 75% in certain extreme scenarios) for popular LLMs like LLaMA2-7B-base and Mistral-7B-v0.3-base.

Improved Operator Learning by Orthogonal Attention

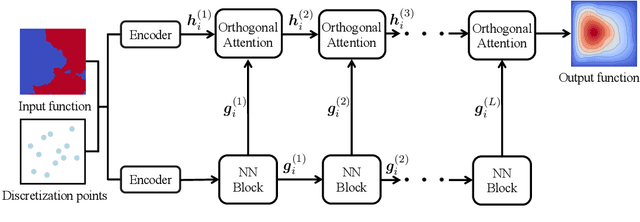
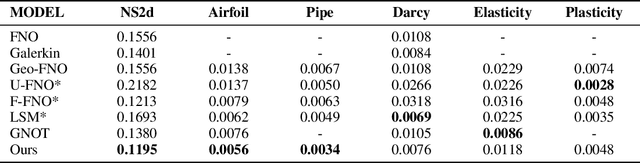
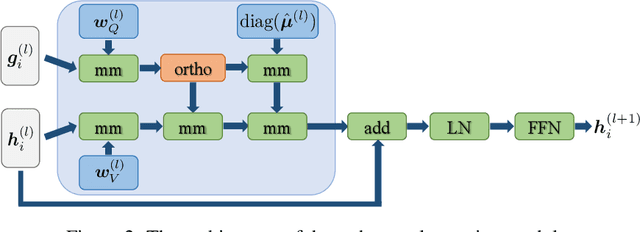
Neural operators, as an efficient surrogate model for learning the solutions of PDEs, have received extensive attention in the field of scientific machine learning. Among them, attention-based neural operators have become one of the mainstreams in related research. However, existing approaches overfit the limited training data due to the considerable number of parameters in the attention mechanism. To address this, we develop an orthogonal attention based on the eigendecomposition of the kernel integral operator and the neural approximation of eigenfunctions. The orthogonalization naturally poses a proper regularization effect on the resulting neural operator, which aids in resisting overfitting and boosting generalization. Experiments on six standard neural operator benchmark datasets comprising both regular and irregular geometries show that our method can outperform competing baselines with decent margins.