Tianqi Hou
LoPA: Scaling dLLM Inference via Lookahead Parallel Decoding
Dec 22, 2025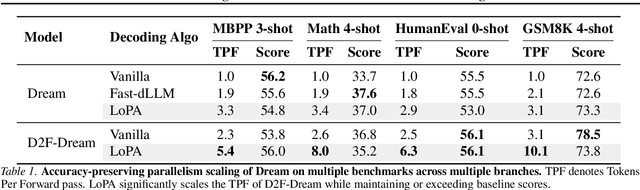
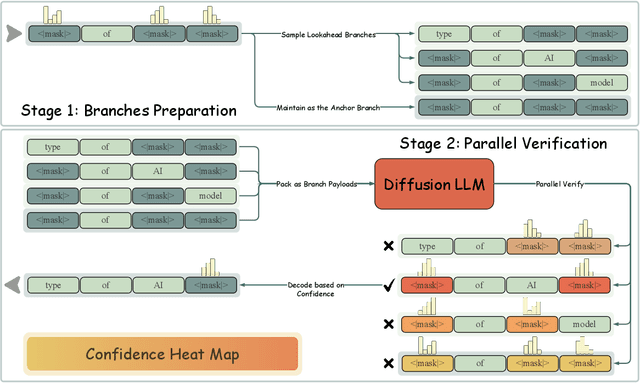
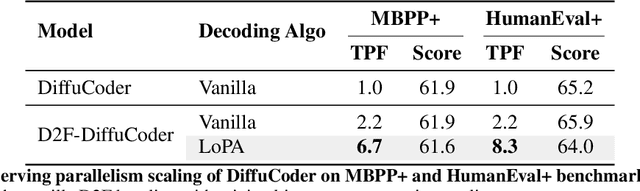
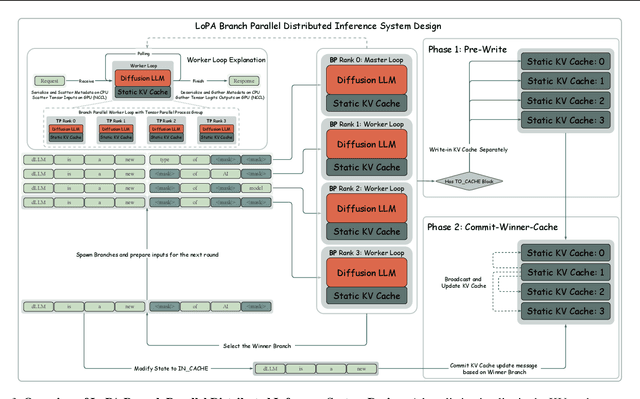
Abstract:Diffusion Large Language Models (dLLMs) have demonstrated significant potential for high-speed inference. However, current confidence-driven decoding strategies are constrained by limited parallelism, typically achieving only 1--3 tokens per forward pass (TPF). In this work, we identify that the degree of parallelism during dLLM inference is highly sensitive to the Token Filling Order (TFO). Then, we introduce Lookahead PArallel Decoding LoPA, a training-free, plug-and-play algorithm, to identify a superior TFO and hence accelerate inference. LoPA concurrently explores distinct candidate TFOs via parallel branches, and selects the one with the highest potential for future parallelism based on branch confidence. We apply LoPA to the state-of-the-art D2F model and observe a substantial enhancement in decoding efficiency. Notably, LoPA increases the TPF of D2F-Dream to 10.1 on the GSM8K while maintaining performance superior to the Dream baseline. Furthermore, to facilitate this unprecedented degree of parallelism, we develop a specialized multi-device inference system featuring Branch Parallelism (BP), which achieves a single-sample throughput of 1073.9 tokens per second under multi-GPU deployment. The code is available at https://github.com/zhijie-group/LoPA.
Show-o Turbo: Towards Accelerated Unified Multimodal Understanding and Generation
Feb 08, 2025Abstract:There has been increasing research interest in building unified multimodal understanding and generation models, among which Show-o stands as a notable representative, demonstrating great promise for both text-to-image and image-to-text generation. The inference of Show-o involves progressively denoising image tokens and autoregressively decoding text tokens, and hence, unfortunately, suffers from inefficiency issues from both sides. This paper introduces Show-o Turbo to bridge the gap. We first identify a unified denoising perspective for the generation of images and text in Show-o based on the parallel decoding of text tokens. We then propose to extend consistency distillation (CD), a qualified approach for shortening the denoising process of diffusion models, to the multimodal denoising trajectories of Show-o. We introduce a trajectory segmentation strategy and a curriculum learning procedure to improve the training convergence. Empirically, in text-to-image generation, Show-o Turbo displays a GenEval score of 0.625 at 4 sampling steps without using classifier-free guidance (CFG), outperforming that of the original Show-o with 8 steps and CFG; in image-to-text generation, Show-o Turbo exhibits a 1.5x speedup without significantly sacrificing performance. The code is available at https://github.com/zhijie-group/Show-o-Turbo.
MatryoshkaKV: Adaptive KV Compression via Trainable Orthogonal Projection
Oct 16, 2024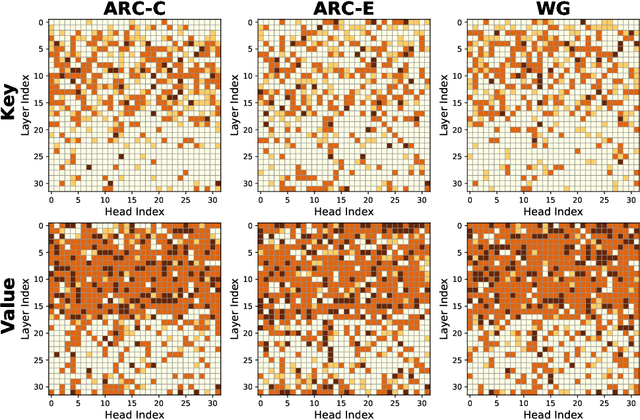



Abstract:KV cache has become a de facto technique for the inference of large language models (LLMs), where tensors of shape (layer number, head number, sequence length, feature dimension) are introduced to cache historical information for self-attention. As the size of the model and data grows, the KV cache can quickly become a bottleneck within the system in both storage and memory transfer. To address this, prior studies usually focus on the first three axes of the cache tensors for compression. This paper supplements them, focusing on the feature dimension axis, by utilizing low-rank projection matrices to transform the cache features into spaces with reduced dimensions. We begin by investigating the canonical orthogonal projection method for data compression through principal component analysis (PCA). We observe the issue with PCA projection where significant performance degradation is observed at low compression rates. To bridge the gap, we propose to directly tune the orthogonal projection matrices with a distillation objective using an elaborate Matryoshka training strategy. After training, we adaptively search for the optimal compression rates for various layers and heads given varying compression budgets. Compared to previous works, our method can easily embrace pre-trained LLMs and hold a smooth tradeoff between performance and compression rate. We empirically witness the high data efficiency of our training procedure and find that our method can sustain over 90% performance with an average KV cache compression rate of 60% (and up to 75% in certain extreme scenarios) for popular LLMs like LLaMA2-7B-base and Mistral-7B-v0.3-base.
In-context KV-Cache Eviction for LLMs via Attention-Gate
Oct 15, 2024



Abstract:The KV-Cache technique has become the standard for the inference of large language models (LLMs). It caches states of self-attention to avoid recomputation. Yet, it is widely criticized that KV-Cache can become a bottleneck of the LLM inference system, especially when confronted with ultra-large models and long-context queries. A natural remedy is to discard the KV-Cache for less important tokens, with StreamingLLM as an example, but the used static eviction strategies cannot flexibly adapt to varying contexts. Remedies like H2O leverage accumulative attention scores to perform dynamic eviction but suffer from the attention bias issue in capturing contextual information. This paper bridges this gap by devising a parameterized KV-Cache eviction mechanism, dubbed as Attention-Gate, which accepts the whole context as input and yields eviction flags for each token to realize in-context eviction. The subsequent self-attention module proceeds according to the flags and only the KV states for the remaining tokens need to be cached. The Attention-Gates can vary among different heads and layers and be trivially plugged into pre-trained LLMs, tuned by cost-effective continual pre-training or supervised fine-tuning objectives to acquire what to discard. The computational and memory overhead introduced by Attention-Gates is minimal. Our method is validated across multiple tasks, demonstrating both efficiency and adaptability. After a highly efficient continual pre-training, it achieves higher average accuracy and evicts more tokens compared to traditional training-free methods. In supervised fine-tuning, it not only evicts many tokens but also outperforms LoRA-finetuned LLMs on some datasets, such as RTE, where it improves accuracy by 13.9% while evicting 62.8% of tokens, showing that effective eviction of redundant tokens can even enhance performance.
Decentralizing Coherent Joint Transmission Precoding via Fast ADMM with Deterministic Equivalents
Mar 28, 2024



Abstract:Inter-cell interference (ICI) suppression is critical for multi-cell multi-user networks. In this paper, we investigate advanced precoding techniques for coordinated multi-point (CoMP) with downlink coherent joint transmission, an effective approach for ICI suppression. Different from the centralized precoding schemes that require frequent information exchange among the cooperating base stations, we propose a decentralized scheme to minimize the total power consumption. In particular, based on the covariance matrices of global channel state information, we estimate the ICI bounds via the deterministic equivalents and decouple the original design problem into sub-problems, each of which can be solved in a decentralized manner. To solve the sub-problems at each base station, we develop a low-complexity solver based on the alternating direction method of multipliers (ADMM) in conjunction with the convex-concave procedure (CCCP). Simulation results demonstrate the effectiveness of our proposed decentralized precoding scheme, which achieves performance similar to the optimal centralized precoding scheme. Besides, our proposed ADMM solver can substantially reduce the computational complexity, while maintaining outstanding performance.
Decentralizing Coherent Joint Transmission Precoding via Deterministic Equivalents
Mar 15, 2024
Abstract:In order to control the inter-cell interference for a multi-cell multi-user multiple-input multiple-output network, we consider the precoder design for coordinated multi-point with downlink coherent joint transmission. To avoid costly information exchange among the cooperating base stations in a centralized precoding scheme, we propose a decentralized one by considering the power minimization problem. By approximating the inter-cell interference using the deterministic equivalents, this problem is decoupled to sub-problems which are solved in a decentralized manner at different base stations. Simulation results demonstrate the effectiveness of our proposed decentralized precoding scheme, where only 2 ~ 7% more transmit power is needed compared with the optimal centralized precoder.
Spectrum of non-Hermitian deep-Hebbian neural networks
Aug 24, 2022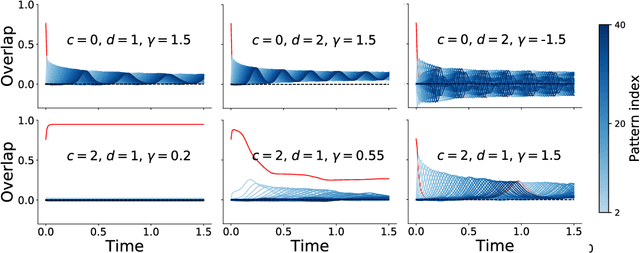
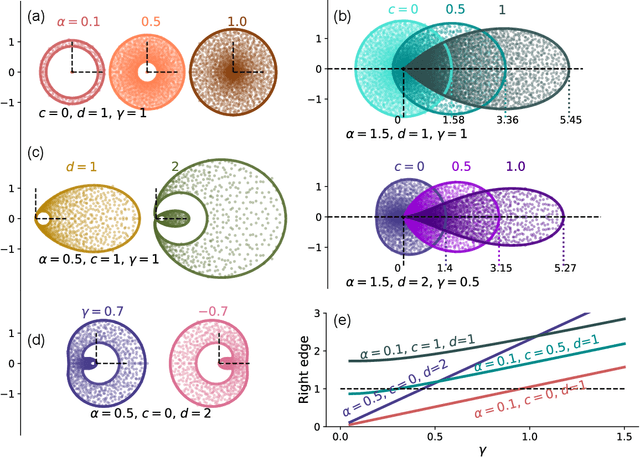
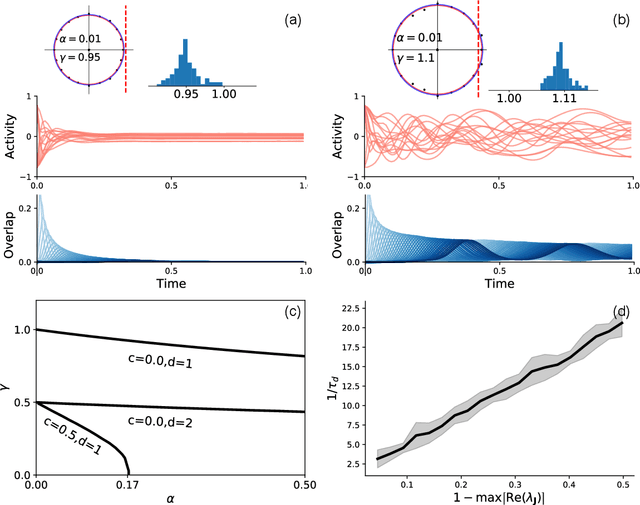
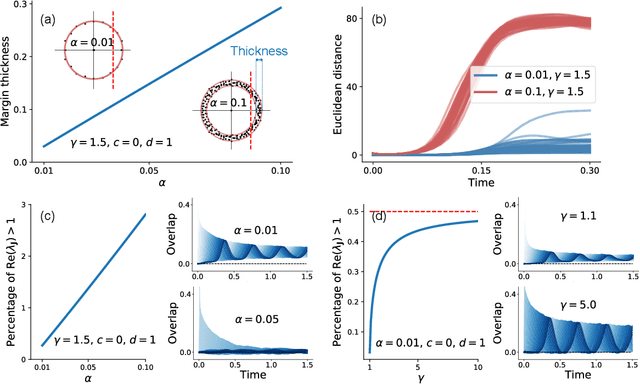
Abstract:Neural networks with recurrent asymmetric couplings are important to understand how episodic memories are encoded in the brain. Here, we integrate the experimental observation of wide synaptic integration window into our model of sequence retrieval in the continuous time dynamics. The model with non-normal neuron-interactions is theoretically studied by deriving a random matrix theory of the Jacobian matrix in neural dynamics. The spectra bears several distinct features, such as breaking rotational symmetry about the origin, and the emergence of nested voids within the spectrum boundary. The spectral density is thus highly non-uniformly distributed in the complex plane. The random matrix theory also predicts a transition to chaos. In particular, the edge of chaos provides computational benefits for the sequential retrieval of memories. Our work provides a systematic study of time-lagged correlations with arbitrary time delays, and thus can inspire future studies of a broad class of memory models, and even big data analysis of biological time series.
Statistical physics of unsupervised learning with prior knowledge in neural networks
Nov 06, 2019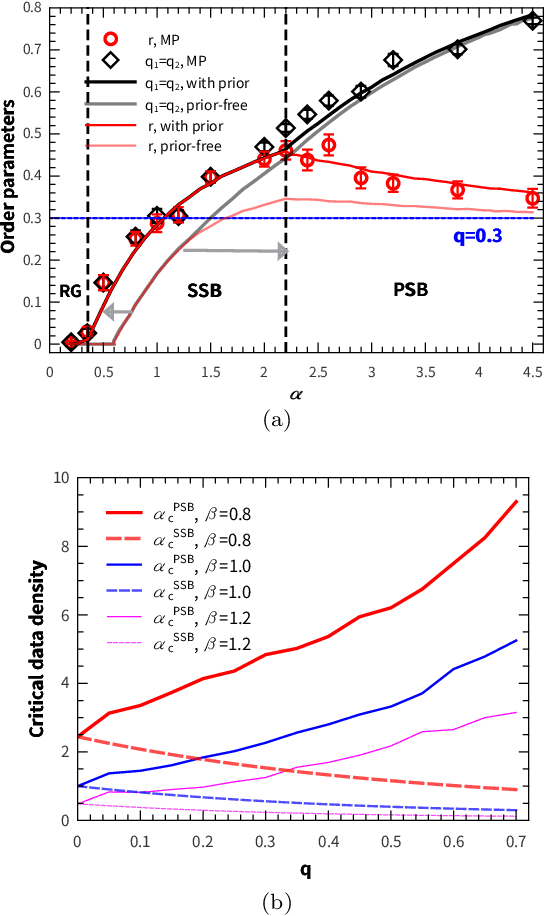
Abstract:Integrating sensory inputs with prior beliefs from past experiences in unsupervised learning is a common and fundamental characteristic of brain or artificial neural computation. However, a quantitative role of prior knowledge in unsupervised learning remains unclear, prohibiting a scientific understanding of unsupervised learning. Here, we propose a statistical physics model of unsupervised learning with prior knowledge, revealing that the sensory inputs drive a series of continuous phase transitions related to spontaneous intrinsic-symmetry breaking. The intrinsic symmetry includes both reverse symmetry and permutation symmetry, commonly observed in most artificial neural networks. Compared to the prior-free scenario, the prior reduces more strongly the minimal data size triggering the reverse symmetry breaking transition, and moreover, the prior merges, rather than separates, permutation symmetry breaking phases. We claim that the prior can be learned from data samples, which in physics corresponds to a two-parameter Nishimori plane constraint. This work thus reveals mechanisms about the influence of the prior on unsupervised learning.
Minimal model of permutation symmetry in unsupervised learning
Apr 30, 2019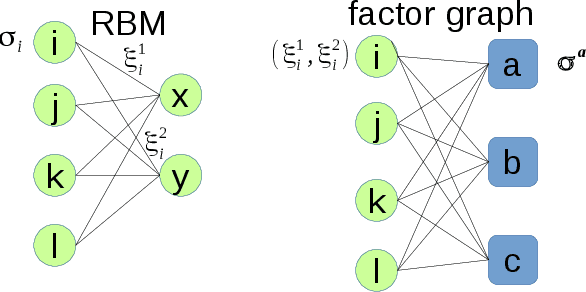

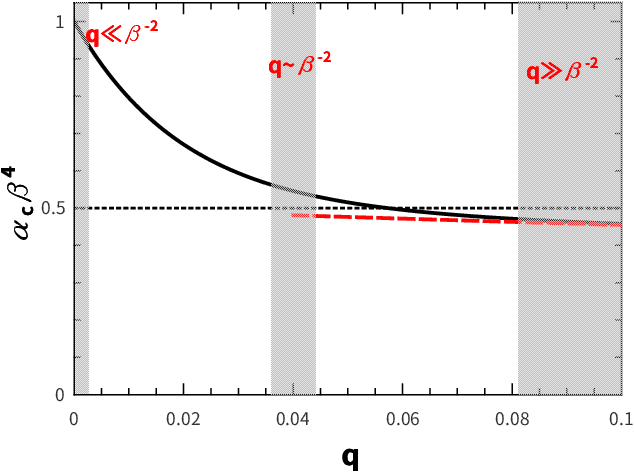
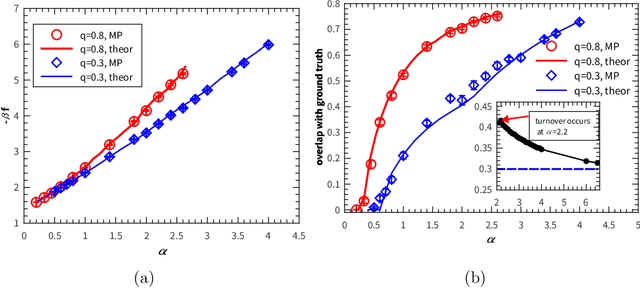
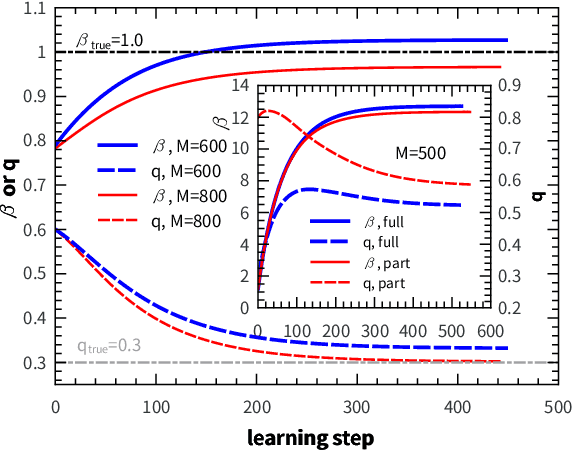
Abstract:Permutation of any two hidden units yields invariant properties in typical deep generative neural networks. This permutation symmetry plays an important role in understanding the computation performance of a broad class of neural networks with two or more hidden units. However, a theoretical study of the permutation symmetry is still lacking. Here, we propose a minimal model with only two hidden units in a restricted Boltzmann machine, which aims to address how the permutation symmetry affects the critical learning data size at which the concept-formation (or spontaneous symmetry breaking in physics language) starts, and moreover semi-rigorously prove a conjecture that the critical data size is independent of the number of hidden units once this number is finite. Remarkably, we find that the embedded correlation between two receptive fields of hidden units reduces the critical data size. In particular, the weakly-correlated receptive fields have the benefit of significantly reducing the minimal data size that triggers the transition, given less noisy data. Inspired by the theory, we also propose an efficient fully-distributed algorithm to infer the receptive fields of hidden units. Overall, our results demonstrate that the permutation symmetry is an interesting property that affects the critical data size for computation performances of related learning algorithms. All these effects can be analytically probed based on the minimal model, providing theoretical insights towards understanding unsupervised learning in a more general context.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge