Minimal model of permutation symmetry in unsupervised learning

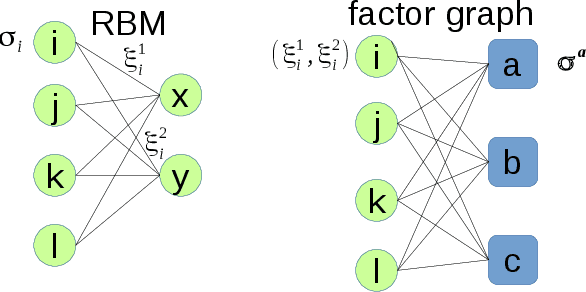
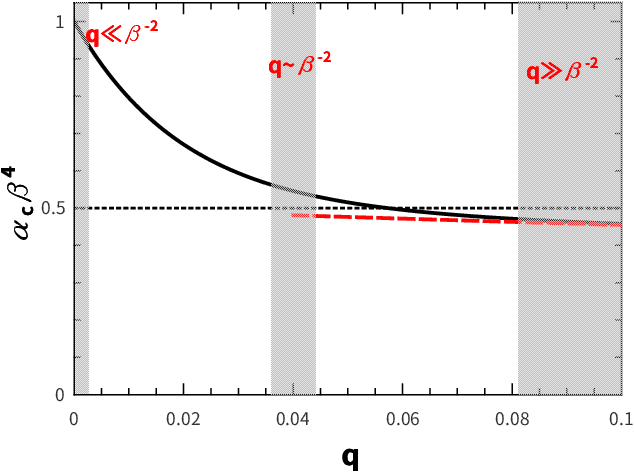
Permutation of any two hidden units yields invariant properties in typical deep generative neural networks. This permutation symmetry plays an important role in understanding the computation performance of a broad class of neural networks with two or more hidden units. However, a theoretical study of the permutation symmetry is still lacking. Here, we propose a minimal model with only two hidden units in a restricted Boltzmann machine, which aims to address how the permutation symmetry affects the critical learning data size at which the concept-formation (or spontaneous symmetry breaking in physics language) starts, and moreover semi-rigorously prove a conjecture that the critical data size is independent of the number of hidden units once this number is finite. Remarkably, we find that the embedded correlation between two receptive fields of hidden units reduces the critical data size. In particular, the weakly-correlated receptive fields have the benefit of significantly reducing the minimal data size that triggers the transition, given less noisy data. Inspired by the theory, we also propose an efficient fully-distributed algorithm to infer the receptive fields of hidden units. Overall, our results demonstrate that the permutation symmetry is an interesting property that affects the critical data size for computation performances of related learning algorithms. All these effects can be analytically probed based on the minimal model, providing theoretical insights towards understanding unsupervised learning in a more general context.

Entropy landscape of solutions in the binary perceptron problem

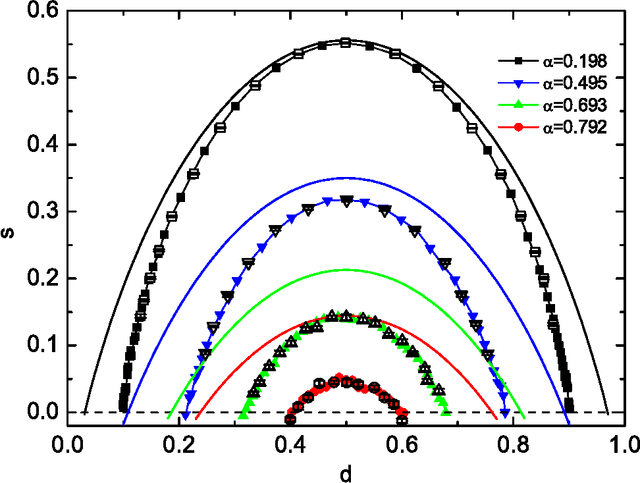
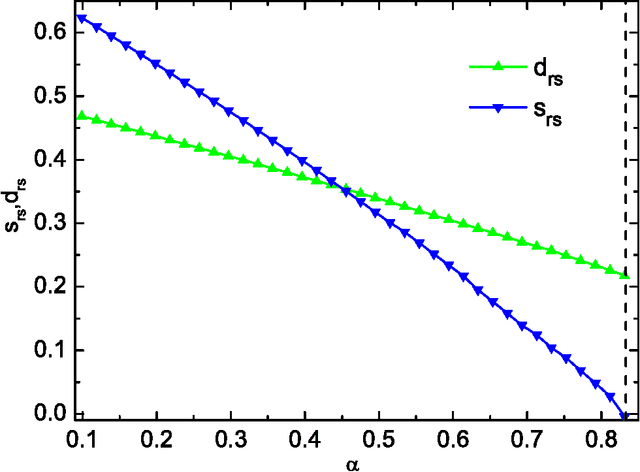
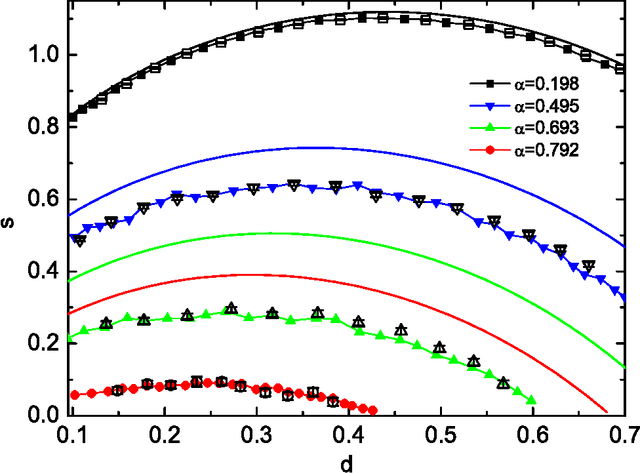
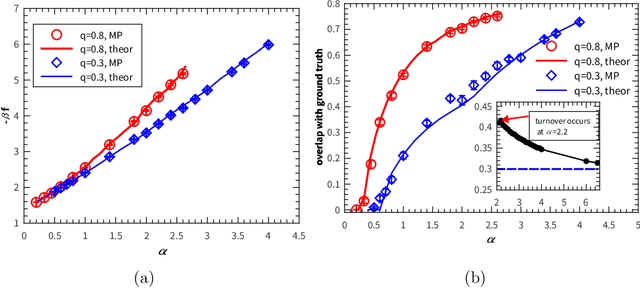
The statistical picture of the solution space for a binary perceptron is studied. The binary perceptron learns a random classification of input random patterns by a set of binary synaptic weights. The learning of this network is difficult especially when the pattern (constraint) density is close to the capacity, which is supposed to be intimately related to the structure of the solution space. The geometrical organization is elucidated by the entropy landscape from a reference configuration and of solution-pairs separated by a given Hamming distance in the solution space. We evaluate the entropy at the annealed level as well as replica symmetric level and the mean field result is confirmed by the numerical simulations on single instances using the proposed message passing algorithms. From the first landscape (a random configuration as a reference), we see clearly how the solution space shrinks as more constraints are added. From the second landscape of solution-pairs, we deduce the coexistence of clustering and freezing in the solution space.