Spectrum of non-Hermitian deep-Hebbian neural networks
Paper and Code
Aug 24, 2022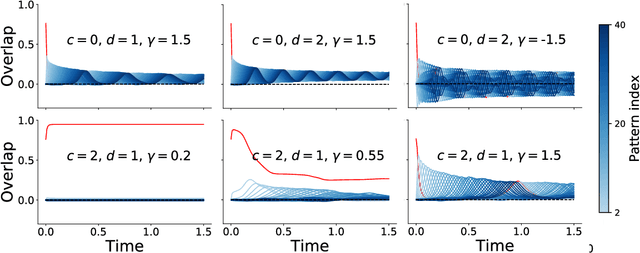
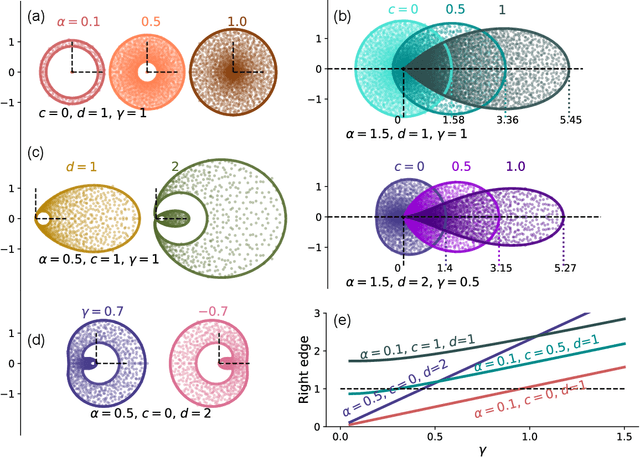
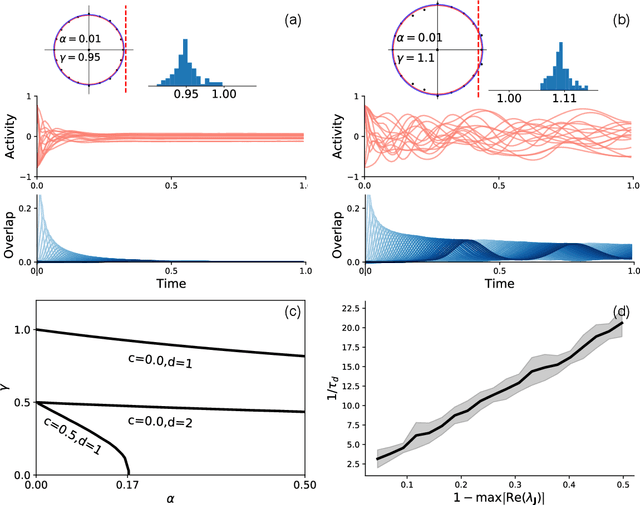
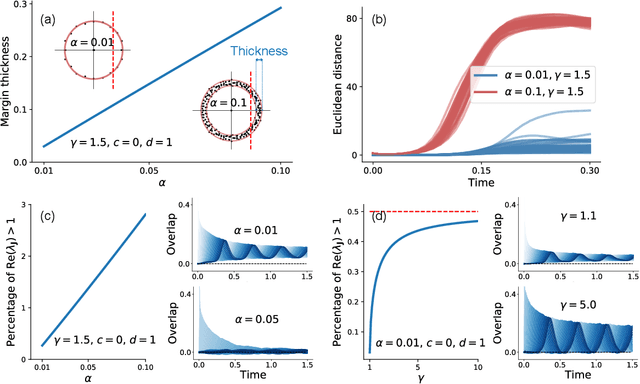
Neural networks with recurrent asymmetric couplings are important to understand how episodic memories are encoded in the brain. Here, we integrate the experimental observation of wide synaptic integration window into our model of sequence retrieval in the continuous time dynamics. The model with non-normal neuron-interactions is theoretically studied by deriving a random matrix theory of the Jacobian matrix in neural dynamics. The spectra bears several distinct features, such as breaking rotational symmetry about the origin, and the emergence of nested voids within the spectrum boundary. The spectral density is thus highly non-uniformly distributed in the complex plane. The random matrix theory also predicts a transition to chaos. In particular, the edge of chaos provides computational benefits for the sequential retrieval of memories. Our work provides a systematic study of time-lagged correlations with arbitrary time delays, and thus can inspire future studies of a broad class of memory models, and even big data analysis of biological time series.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge