Track4Action: Distilling World-Centric 3D Tracker into Vision-Language-Action Policies

Action labels tell a vision-language-action (VLA) policy which robot commands to imitate, but not how those commands change the 3D world. The aligned demonstration clip contains this missing supervision because its $K$ frame transitions record the geometry, motion, visibility, and camera change produced during the corresponding $K$ actions. We introduce Track4Action, a framework that distills this realized transition from a frozen world-centric 3D tracker into a current-observation VLA policy. During training, Track4World encodes the clip $V_{t:t+K}$ into a pooled tracker feature. Learnable track queries infer this feature from current VLA hidden states, match it in a shared space, and condition a flow-matching action head through a feature-wise gate. The tracker feature only defines the alignment target, so neither the clip nor the tracker is used at deployment. Track4Action reaches 82.3% on zero-shot LIBERO-Plus, improving the alignment-free variant by 7.6 points and LaMP by 3.0 points. It obtains 80.44% and 81.48% on the clean and randomized RoboTwin 2.0 splits, and 67.5% average success across four physical bimanual tasks, 25.0 points above the alignment-free variant. The gains across simulation and physical tasks support action-aligned 3D tracker features as privileged supervision for tracker-free VLA deployment. Our project page is available at https://wing0night.github.io/track4action-project-page.

ChronoFlow-Policy: Unifying Past-Current-Future Interaction Flow in Visuomotor Policy Learning

Visual signals play a crucial role in policy learning by enabling models to capture object motion and interaction dynamics. Just as humans reason about actions using both past experience and anticipated outcomes, effective policies should integrate past interactions with future predictions. However, existing visuomotor policies typically model either historical context or future dynamics in isolation, lacking a unified temporal representation of interaction dynamics. In this work, we introduce \textbf{ChronoFlow}, a temporally unified representation that captures \textbf{past, current, and future} interaction dynamics through sparse 3D keypoints of both objects and the gripper. Based on this representation, we propose \textbf{ChronoFlow-Policy}, a diffusion-based visuomotor policy that jointly learns ChronoFlow and action sequences through a co-training objective. Experiments on 14 simulated tasks and 5 real-world manipulation tasks demonstrate that ChronoFlow-Policy consistently outperforms strong diffusion-policy baselines and improves robustness in long-horizon and non-Markovian manipulation scenarios.

LIDEA: Human-to-Robot Imitation Learning via Implicit Feature Distillation and Explicit Geometry Alignment

Scaling up robot learning is hindered by the scarcity of robotic demonstrations, whereas human videos offer a vast, untapped source of interaction data. However, bridging the embodiment gap between human hands and robot arms remains a critical challenge. Existing cross-embodiment transfer strategies typically rely on visual editing, but they often introduce visual artifacts due to intrinsic discrepancies in visual appearance and 3D geometry. To address these limitations, we introduce LIDEA (Implicit Feature Distillation and Explicit Geometric Alignment), an imitation learning framework in which policy learning benefits from human demonstrations. In the 2D visual domain, LIDEA employs a dual-stage transitive distillation pipeline that aligns human and robot representations in a shared latent space. In the 3D geometric domain, we propose an embodiment-agnostic alignment strategy that explicitly decouples embodiment from interaction geometry, ensuring consistent 3D-aware perception. Extensive experiments empirically validate LIDEA from two perspectives: data efficiency and OOD robustness. Results show that human data substitutes up to 80% of costly robot demonstrations, and the framework successfully transfers unseen patterns from human videos for out-of-distribution generalization.

MatryoshkaKV: Adaptive KV Compression via Trainable Orthogonal Projection

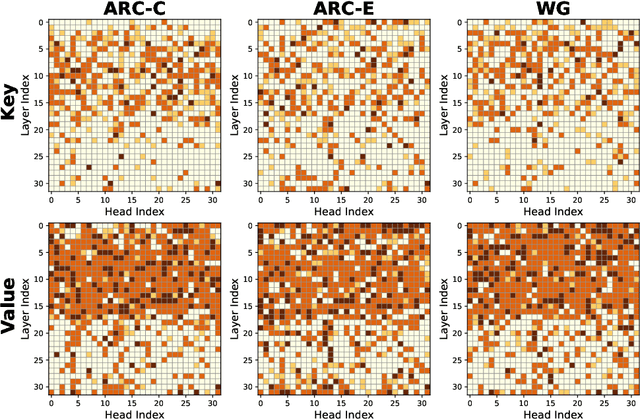
KV cache has become a de facto technique for the inference of large language models (LLMs), where tensors of shape (layer number, head number, sequence length, feature dimension) are introduced to cache historical information for self-attention. As the size of the model and data grows, the KV cache can quickly become a bottleneck within the system in both storage and memory transfer. To address this, prior studies usually focus on the first three axes of the cache tensors for compression. This paper supplements them, focusing on the feature dimension axis, by utilizing low-rank projection matrices to transform the cache features into spaces with reduced dimensions. We begin by investigating the canonical orthogonal projection method for data compression through principal component analysis (PCA). We observe the issue with PCA projection where significant performance degradation is observed at low compression rates. To bridge the gap, we propose to directly tune the orthogonal projection matrices with a distillation objective using an elaborate Matryoshka training strategy. After training, we adaptively search for the optimal compression rates for various layers and heads given varying compression budgets. Compared to previous works, our method can easily embrace pre-trained LLMs and hold a smooth tradeoff between performance and compression rate. We empirically witness the high data efficiency of our training procedure and find that our method can sustain over 90% performance with an average KV cache compression rate of 60% (and up to 75% in certain extreme scenarios) for popular LLMs like LLaMA2-7B-base and Mistral-7B-v0.3-base.

In-context KV-Cache Eviction for LLMs via Attention-Gate

The KV-Cache technique has become the standard for the inference of large language models (LLMs). It caches states of self-attention to avoid recomputation. Yet, it is widely criticized that KV-Cache can become a bottleneck of the LLM inference system, especially when confronted with ultra-large models and long-context queries. A natural remedy is to discard the KV-Cache for less important tokens, with StreamingLLM as an example, but the used static eviction strategies cannot flexibly adapt to varying contexts. Remedies like H2O leverage accumulative attention scores to perform dynamic eviction but suffer from the attention bias issue in capturing contextual information. This paper bridges this gap by devising a parameterized KV-Cache eviction mechanism, dubbed as Attention-Gate, which accepts the whole context as input and yields eviction flags for each token to realize in-context eviction. The subsequent self-attention module proceeds according to the flags and only the KV states for the remaining tokens need to be cached. The Attention-Gates can vary among different heads and layers and be trivially plugged into pre-trained LLMs, tuned by cost-effective continual pre-training or supervised fine-tuning objectives to acquire what to discard. The computational and memory overhead introduced by Attention-Gates is minimal. Our method is validated across multiple tasks, demonstrating both efficiency and adaptability. After a highly efficient continual pre-training, it achieves higher average accuracy and evicts more tokens compared to traditional training-free methods. In supervised fine-tuning, it not only evicts many tokens but also outperforms LoRA-finetuned LLMs on some datasets, such as RTE, where it improves accuracy by 13.9% while evicting 62.8% of tokens, showing that effective eviction of redundant tokens can even enhance performance.

Improved Operator Learning by Orthogonal Attention

Neural operators, as an efficient surrogate model for learning the solutions of PDEs, have received extensive attention in the field of scientific machine learning. Among them, attention-based neural operators have become one of the mainstreams in related research. However, existing approaches overfit the limited training data due to the considerable number of parameters in the attention mechanism. To address this, we develop an orthogonal attention based on the eigendecomposition of the kernel integral operator and the neural approximation of eigenfunctions. The orthogonalization naturally poses a proper regularization effect on the resulting neural operator, which aids in resisting overfitting and boosting generalization. Experiments on six standard neural operator benchmark datasets comprising both regular and irregular geometries show that our method can outperform competing baselines with decent margins.