Improved Operator Learning by Orthogonal Attention
Paper and Code
Oct 23, 2023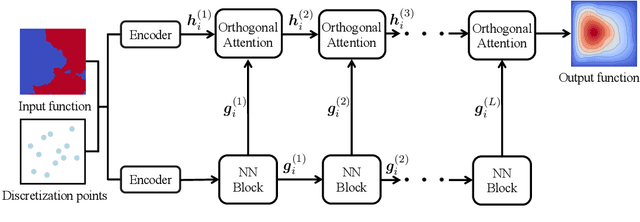
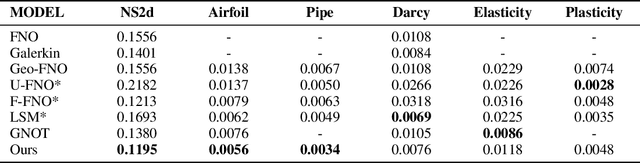
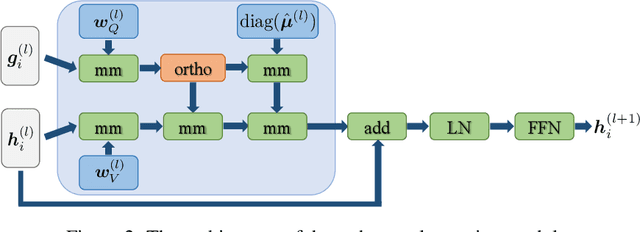

Neural operators, as an efficient surrogate model for learning the solutions of PDEs, have received extensive attention in the field of scientific machine learning. Among them, attention-based neural operators have become one of the mainstreams in related research. However, existing approaches overfit the limited training data due to the considerable number of parameters in the attention mechanism. To address this, we develop an orthogonal attention based on the eigendecomposition of the kernel integral operator and the neural approximation of eigenfunctions. The orthogonalization naturally poses a proper regularization effect on the resulting neural operator, which aids in resisting overfitting and boosting generalization. Experiments on six standard neural operator benchmark datasets comprising both regular and irregular geometries show that our method can outperform competing baselines with decent margins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge