Statistical physics of unsupervised learning with prior knowledge in neural networks

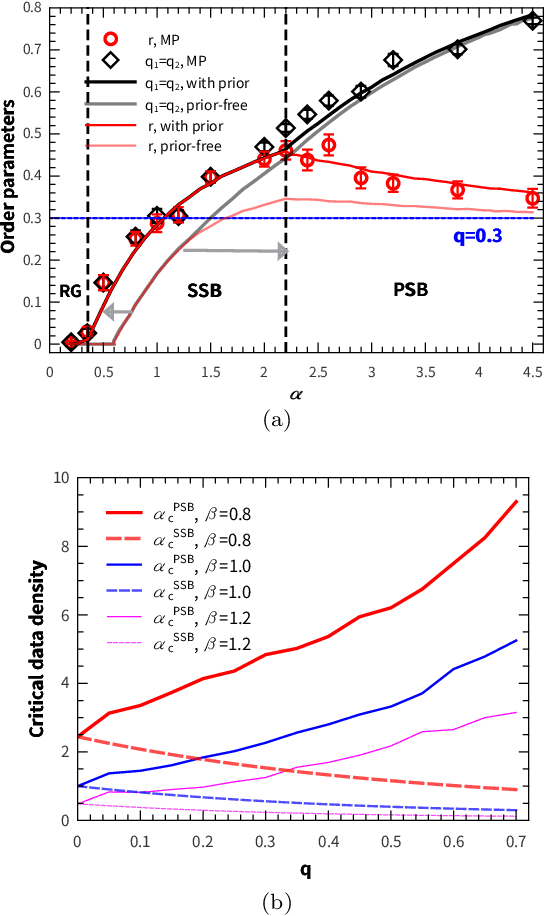
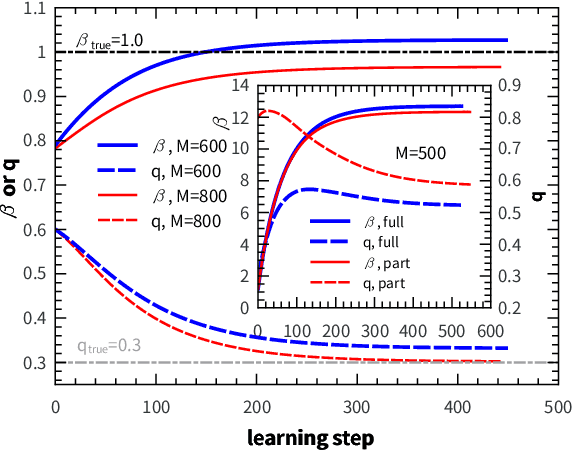
Integrating sensory inputs with prior beliefs from past experiences in unsupervised learning is a common and fundamental characteristic of brain or artificial neural computation. However, a quantitative role of prior knowledge in unsupervised learning remains unclear, prohibiting a scientific understanding of unsupervised learning. Here, we propose a statistical physics model of unsupervised learning with prior knowledge, revealing that the sensory inputs drive a series of continuous phase transitions related to spontaneous intrinsic-symmetry breaking. The intrinsic symmetry includes both reverse symmetry and permutation symmetry, commonly observed in most artificial neural networks. Compared to the prior-free scenario, the prior reduces more strongly the minimal data size triggering the reverse symmetry breaking transition, and moreover, the prior merges, rather than separates, permutation symmetry breaking phases. We claim that the prior can be learned from data samples, which in physics corresponds to a two-parameter Nishimori plane constraint. This work thus reveals mechanisms about the influence of the prior on unsupervised learning.