Noisy Computing of the $\mathsf{OR}$ and $\mathsf{MAX}$ Functions

We consider the problem of computing a function of $n$ variables using noisy queries, where each query is incorrect with some fixed and known probability $p \in (0,1/2)$. Specifically, we consider the computation of the $\mathsf{OR}$ function of $n$ bits (where queries correspond to noisy readings of the bits) and the $\mathsf{MAX}$ function of $n$ real numbers (where queries correspond to noisy pairwise comparisons). We show that an expected number of queries of \[ (1 \pm o(1)) \frac{n\log \frac{1}{\delta}}{D_{\mathsf{KL}}(p \| 1-p)} \] is both sufficient and necessary to compute both functions with a vanishing error probability $\delta = o(1)$, where $D_{\mathsf{KL}}(p \| 1-p)$ denotes the Kullback-Leibler divergence between $\mathsf{Bern}(p)$ and $\mathsf{Bern}(1-p)$ distributions. Compared to previous work, our results tighten the dependence on $p$ in both the upper and lower bounds for the two functions.

FinVis-GPT: A Multimodal Large Language Model for Financial Chart Analysis

In this paper, we propose FinVis-GPT, a novel multimodal large language model (LLM) specifically designed for financial chart analysis. By leveraging the power of LLMs and incorporating instruction tuning and multimodal capabilities, FinVis-GPT is capable of interpreting financial charts and providing valuable analysis. To train FinVis-GPT, a financial task oriented dataset was generated for pre-training alignment and instruction tuning, comprising various types of financial charts and their corresponding descriptions. We evaluate the model performance via several case studies due to the time limit, and the promising results demonstrated that FinVis-GPT is superior in various financial chart related tasks, including generating descriptions, answering questions and predicting future market trends, surpassing existing state-of-the-art multimodal LLMs. The proposed FinVis-GPT serves as a pioneering effort in utilizing multimodal LLMs in the finance domain and our generated dataset will be release for public use in the near future to speedup related research.

An Effective Data Creation Pipeline to Generate High-quality Financial Instruction Data for Large Language Model

At the beginning era of large language model, it is quite critical to generate a high-quality financial dataset to fine-tune a large language model for financial related tasks. Thus, this paper presents a carefully designed data creation pipeline for this purpose. Particularly, we initiate a dialogue between an AI investor and financial expert using ChatGPT and incorporate the feedback of human financial experts, leading to the refinement of the dataset. This pipeline yielded a robust instruction tuning dataset comprised of 103k multi-turn chats. Extensive experiments have been conducted on this dataset to evaluate the model's performance by adopting an external GPT-4 as the judge. The promising experimental results verify that our approach led to significant advancements in generating accurate, relevant, and financial-style responses from AI models, and thus providing a powerful tool for applications within the financial sector.

On the Optimal Bounds for Noisy Computing

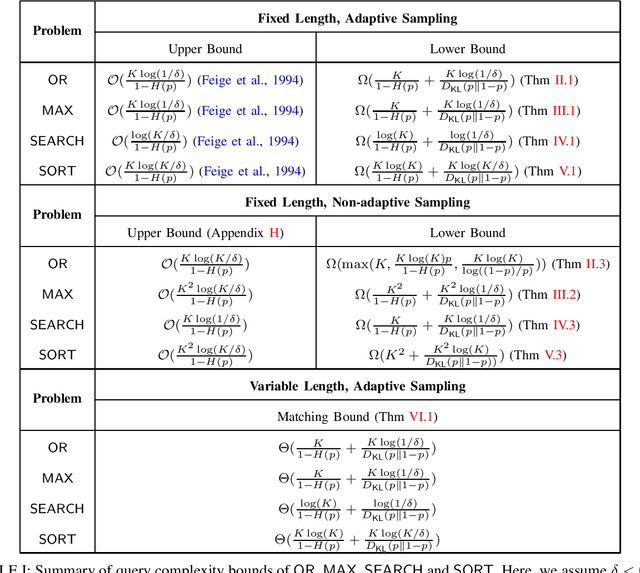
We revisit the problem of computing with noisy information considered in Feige et al. 1994, which includes computing the OR function from noisy queries, and computing the MAX, SEARCH and SORT functions from noisy pairwise comparisons. For $K$ given elements, the goal is to correctly recover the desired function with probability at least $1-\delta$ when the outcome of each query is flipped with probability $p$. We consider both the adaptive sampling setting where each query can be adaptively designed based on past outcomes, and the non-adaptive sampling setting where the query cannot depend on past outcomes. The prior work provides tight bounds on the worst-case query complexity in terms of the dependence on $K$. However, the upper and lower bounds do not match in terms of the dependence on $\delta$ and $p$. We improve the lower bounds for all the four functions under both adaptive and non-adaptive query models. Most of our lower bounds match the upper bounds up to constant factors when either $p$ or $\delta$ is bounded away from $0$, while the ratio between the best prior upper and lower bounds goes to infinity when $p\rightarrow 0$ or $p\rightarrow 1/2$. On the other hand, we also provide matching upper and lower bounds for the number of queries in expectation, improving both the upper and lower bounds for the variable-length query model.

PINNacle: A Comprehensive Benchmark of Physics-Informed Neural Networks for Solving PDEs

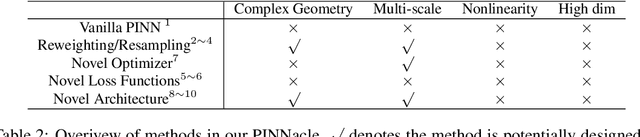
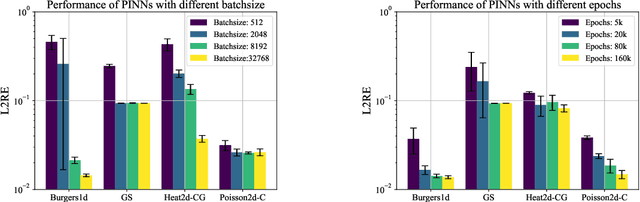
While significant progress has been made on Physics-Informed Neural Networks (PINNs), a comprehensive comparison of these methods across a wide range of Partial Differential Equations (PDEs) is still lacking. This study introduces PINNacle, a benchmarking tool designed to fill this gap. PINNacle provides a diverse dataset, comprising over 20 distinct PDEs from various domains including heat conduction, fluid dynamics, biology, and electromagnetics. These PDEs encapsulate key challenges inherent to real-world problems, such as complex geometry, multi-scale phenomena, nonlinearity, and high dimensionality. PINNacle also offers a user-friendly toolbox, incorporating about 10 state-of-the-art PINN methods for systematic evaluation and comparison. We have conducted extensive experiments with these methods, offering insights into their strengths and weaknesses. In addition to providing a standardized means of assessing performance, PINNacle also offers an in-depth analysis to guide future research, particularly in areas such as domain decomposition methods and loss reweighting for handling multi-scale problems and complex geometry. While PINNacle does not guarantee success in all real-world scenarios, it represents a significant contribution to the field by offering a robust, diverse, and comprehensive benchmark suite that will undoubtedly foster further research and development in PINNs.

Probing Negative Sampling Strategies to Learn GraphRepresentations via Unsupervised Contrastive Learning

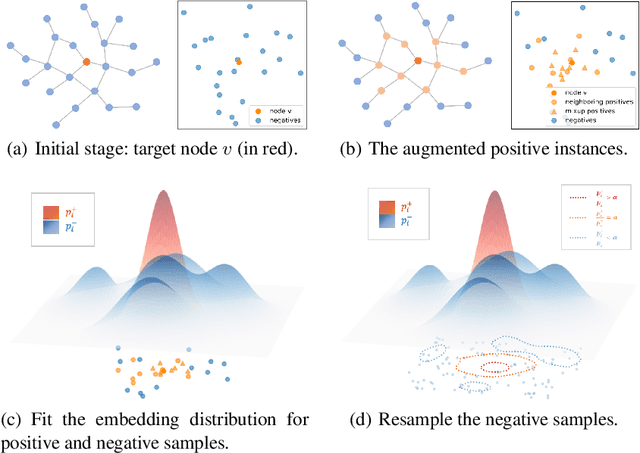
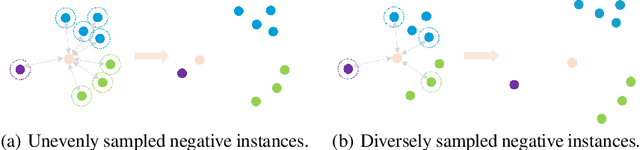
Graph representation learning has long been an important yet challenging task for various real-world applications. However, their downstream tasks are mainly performed in the settings of supervised or semi-supervised learning. Inspired by recent advances in unsupervised contrastive learning, this paper is thus motivated to investigate how the node-wise contrastive learning could be performed. Particularly, we respectively resolve the class collision issue and the imbalanced negative data distribution issue. Extensive experiments are performed on three real-world datasets and the proposed approach achieves the SOTA model performance.

Generating Long Financial Report using Conditional Variational Autoencoders with Knowledge Distillation

Automatically generating financial report from a piece of news is quite a challenging task. Apparently, the difficulty of this task lies in the lack of sufficient background knowledge to effectively generate long financial report. To address this issue, this paper proposes the conditional variational autoencoders (CVAE) based approach which distills external knowledge from a corpus of news-report data. Particularly, we choose Bi-GRU as the encoder and decoder component of CVAE, and learn the latent variable distribution from input news. A higher level latent variable distribution is learnt from a corpus set of news-report data, respectively extr acted for each input news, to provide background knowledge to previously learnt latent variable distribution. Then, a teacher-student network is employed to distill knowledge to refine theoutput of the decoder component. To evaluate the model performance of the proposed approach, extensive experiments are preformed on a public dataset and two widely adopted evaluation criteria, i.e., BLEU and ROUGE, are chosen in the experiment. The promising experimental results demonstrate that the proposed approach is superior to the rest compared methods.