On the Optimal Bounds for Noisy Computing
Paper and Code
Jun 21, 2023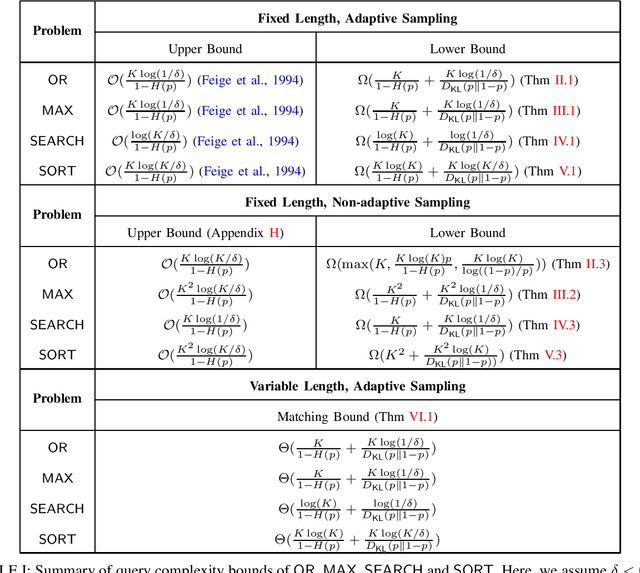
We revisit the problem of computing with noisy information considered in Feige et al. 1994, which includes computing the OR function from noisy queries, and computing the MAX, SEARCH and SORT functions from noisy pairwise comparisons. For $K$ given elements, the goal is to correctly recover the desired function with probability at least $1-\delta$ when the outcome of each query is flipped with probability $p$. We consider both the adaptive sampling setting where each query can be adaptively designed based on past outcomes, and the non-adaptive sampling setting where the query cannot depend on past outcomes. The prior work provides tight bounds on the worst-case query complexity in terms of the dependence on $K$. However, the upper and lower bounds do not match in terms of the dependence on $\delta$ and $p$. We improve the lower bounds for all the four functions under both adaptive and non-adaptive query models. Most of our lower bounds match the upper bounds up to constant factors when either $p$ or $\delta$ is bounded away from $0$, while the ratio between the best prior upper and lower bounds goes to infinity when $p\rightarrow 0$ or $p\rightarrow 1/2$. On the other hand, we also provide matching upper and lower bounds for the number of queries in expectation, improving both the upper and lower bounds for the variable-length query model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge